Випадкові змінні х та у стохастично залежні, якщо зміна однієї з них викликає зміну розподілу другої (умовний розподіл однієї з них залежить від значень другої).

Під час проведення експерніментів стохастичний зв’язок проявляється у тому, що при одному й тому самому значенні однієї змінної отримують різні значення другої, до того ж цей набір значень змінюється зі зміною значень першої змінної. Цей процес між випадковими змінними х та у називають статистичним зв’язком.

Приклад 1. Нехай х – величина основних засобів підприємства, у – річний прибуток підприємства. Припустимо, що на кожному з 5 різних підприємств основні засоби оцінюються в 1 млн грн, а річні прибутки цих підприємств становлять 200тис. грн, 400 тис. грн, 250 тис. грн, 350 тис. грн, 600 тис. грн. Якщо за одиницю вимірювання величини основних засобів та річного прибутку підприємств взяти 1000 грн, то при значенні х = 1000 змінна у набуває набору значень у ₁ = 200; у ₂ = 400; у ₃ = 250; у ₄ = 350; у ₅ = 600. Якщо взяти інші 5 підприємств, наприклад,зосновними засобами по 2 млн грн (х – 2000), то набір значень змінної у зміниться.

Якщо випадкові змінні х та у пов’язані стохастично, то кожному значенню змінної х з області визначення відповідає не одне значення змінної у, а розподіл значень у, який змінюється разом із змінною х, і навпаки: кожне значення у – наслідок не одного значення х, а розподілу значень змінної х. Прикладом стохастичного зв’язку є випадкові функції.

(Означення ВВ)... Щоб описати розподіл випадкової змінної, використлвують функціональні та кількісні характеристики.

Функціональні:

· функція розподілу;

· диференціальна функція (щільність) розподілу.

Кількісні:

· математичне сподівання (середнє значення);

· дисперсія;

· середнє квадратичне відхилення (стандарт);

· моменти (початкові, центральні та ін.);

· мода;

· медіана.

· До кількісних характеристик двох випадкових змінних належить коваріація (змішана дисперсія) та кореляція.

Серенє значення – кількісна характеристика випадкової змінної, котру широко використовують в статистиці. Виділяють такий вид зв’язку між двома випадковими змінними, при якому зміна значень однієї з них призводить до зміни середнього значення другої. Такий вид стохастичної залежності називають кореляційною залежністю. За її допомогою можна кількісно виміряти силу, тісноту цього зв’язку.

При кореляційній залежності, як і при будь-якій іншій стохастичній залежності, кожному значенню факторної змінної х відповідає не одне, а кілька значень результуючої змінної у.

Приклад 2. Для даних прикладу 1 знайдемо умовне середнє значення результуючої змінної у за умови, що факторна ознака х прийме значення, яке дорівнює 1000,-

=360 тис. грн.

Дамо ще одне означення кореляційної залежноті:

Кореляційною залежністю випадкової змінної у від випадкової змінної х називають зв’язок між умовним середнім значенням та відповідним х_і.

Якщо цей зв’язок можна виразити як функціональну залежність рівнянням

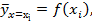
де – деяка відома функція,

то це рівняння називають рівнянням регресії у на х.

Коркляційна залежнсть у від х – це функціональна залежність умовного середнього значення 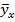від змінної х:

Це рівняння називають рівнянням регресії у на х, функцію f(х) називають регресією у на х, а її графік - теоретичною лінією регресії у на х.

В економетрії термін «рівняння регресії» є синонімом до терміна «рівняння кореляційного зв’язку».

Дата добавления: 2015-10-16