Розв’язання. Встановимо належність змінних до груп незалежних і залежних: за незалежні (вхідні

Встановимо належність змінних до груп незалежних і залежних: за незалежні (вхідні дані) змінні х приймаються доходи населення, а за незалежну (результативну) у – роздрібний товарообіг.

Для специфікації економетричної моделі побудуємо графічне зображення залежності фактичних змінних.

Рис. Фактичні дані та теоретична залежність економетричної моделі.

Зрисунку видно, що це лінійна залежність для парної регресії. Економетрична модель приймає форму

Де – розрахункові значення роздрібного товарообігу;

– оцінки параметрів моделі;

u – випадкова складова (залишки).

Складемо таблицю для побудови моделі:

№	y	x	x^2	xy
					16,67
					18,31
					19,31
					19,25
					21,59
					22,41
					24,05
					24,87
					25,69
					27,33

Оцінемо параметри теоретичної моделі за допомогою метода найменших квадратів. Для цього запишемо систему рівнянь парної регресії для даної задачі:

Підставляємо значення з таблиці в систему рівнянь

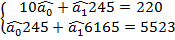
Звідки за формулами

₁ = ; ₀ = - .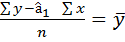

Розв’язавши систему отримаємо

= 1,91; = 0,82.

Економетрична модель має вигляд:

Параметр = 0,82 характеризує граничний розмір витрат на купівлю товарів у роздрібній торгівлі. Тобто, коли дохід збільшується на 1, то обсяг роздрібного товару зросте на 0,82 одиниці: = .

При цьому можна визначити коефіцієнт еластичності (відносний ефект впливу фактора х на результат у) роздрібного товарообігу залежно від доходів населення:

=0,82: (20/24,5)=0,82:0,898=0,91.

Коефіцієнт еластичності показує, на скільки процентів у середньому зміниться результат у зі зміною фактора ч на 1 %. (Зі збільшенням доходів на 1% роздрібний товарообіг зросте на 0,91%.

Дата добавления: 2015-10-16