Цепи синусоидального тока. Метод комплексных амплитуд (МКА). Закон Ома в комплексной форме.

Гармонический ток i(T)=I₀ sin(ωt+φ) которое меняется по данному синусу, является частным случием переменного тока.

I₀ –амплитуда гармонического тока

φ – начальная фаза

рассматривая электрические цепи в которых токи и напряжения меняются по гармоническому закону с одинаковой циклической частотой ω и отличаются только амплитудами а начальными фазами.

ω=2πf

f – частота Гц

T=1/f,с - период колебаний

МКА

Комплексное число z = x+iy; i=sqr(-1)

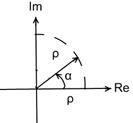ρ = sqr(x² + y²) – модуль комплексного числа

α = y/x = Im(z) / Re(z) – аргумент комплексного числа

отложим вектор ρ вещественной оси

комплексное число z в последовательной форме

z = ρ * e^iα на угол α против часовой стрелки и рассматривать как вектор ρ тложеный на вещественный вектор и повернутый.

Пусть

α(t) = ωt +φ

рассмотрим комплексную формулу от времени

A(t) =A₀e^iα(t) – A₀e^{(ω * t + φ)}

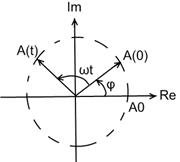
e^(jωt) – оператор вращения с постоянной угловой скоростью ω вектора А(0) против часовой стрелки

e ^{j α} = cos(α) + j * sin(ωt +φ)

посчитаем Im(t) = A₀ * sin(ωt +φ)

A(0) = A – A₀ e ^jφ – комплексная амплитуда гармонического колебания которое полностью его характеризует.

Правило перехода к функции времени:

A(t) = Im(A e ^jωt)

Дата добавления: 2015-10-21