Электроемкость. Конденсаторы. Энергия заряженного конденсатора.

Способность проводников накапливать электрический заряд называется электроемкостью. Если приложить разность потенциалов U к системе проводников, то на них появится заряд q. Опыт показывает, что эти величины связаны линейной зависимостью q ∼ U. Коэффициент пропорциональности в этой зависимости называется электроемкостью С: q= CU. Система из нескольких проводников (не менее двух) называется конденсатором. Чтобы определить электроемкость системы проводников необходимо поместить на низ заряд q и вычислить разность потенциалов U, тогда электроемкость можно определить как С = q/U. Проделаем эти действия для нахождения емкости следующих систем:

Плоский конденсатор (заполнен диэлектриком с диэлектрической проницаемостью ε). На рисунке изображены силовые линии поля каждой пластину. Вне области между плоскостями поля вычитаются, а внутри электрические поля складываются, тогда

; Eвнутр=Eq- Зная, что , получаем U=qb/(ee0S). Тогда C=q/U=ee0S/d. Где S- площадь пластин, d- расстояние м/у ними.

2) Сферический конденсатор (радиусы обкладок R₁ и R₂, между ними – диэлектрик с диэлектрической проницаемостью ε). Поместим на внутреннюю обкладку заряд q, а на внешнюю заряд -q. Найдем по теореме Гаусса поле во всем пространстве. Поле в области пространства r < R₁ равно нулю, так как сферическая поверхность с центром в точке О такого радиуса никаких зарядов не охватывает, и, следовательно, .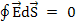

Аналогичная ситуация и в области пространства r > R₂. Только в этом случае полный охватываемый заряд равен нулю. Таким образом, поле есть только в пространстве между обкладками и его найдем по теореме Гаусса(считая, что диэлектрика нет), выбрав для интегрирования сферу радиусом R₁ < r < R₂: .

Тогда с учетом диэлектрика E=q/4piE0Er^2. Разность потенциалов найдем интегрированием

Для электроемкости С=q/U, C=4piEE0* R1R2/R2-R1. Если внешняя сфера имеет бесконечный радиус, то получается конденсаторв виде шара в диэлектрике. Емкость такого шара= С=4piEE0R

3) Цилиндрический конденсатор (высота Н, радиусы обкладок R₁,R₂, внутри диэлектрик ε). Чтобы

формулы были простыми, необходимо предположить, что H >> R₁,R₂ и R₁,R₂ >> R₂ - R₁. Снова

заряжаем конденсатор: внутреннюю обкладку зарядом q, а внешнюю – зарядом –q. Далее в

качестве поверхности для интегрирования выбираем замкнутый цилиндр радиусом R₁ < r < R₂,

охватывающий всю внутреннюю обкладку. Силовые линии электрического поля будут пересекать!

лишь боковую поверхность этого цилиндра и поток вектора D будет равен:

. Теперь определим разность потенциалов . Электроемкость С=2piEE0H?/ln(R2/R1)

Дата добавления: 2015-10-21