Диэлектрики в электрическом поле

Установим метровую деревянную линейку на подставку, обеспечивающую возможность вращения вокруг вертикальной оси. Выполним такой же опыт, как с металлической трубой и заряженной палочкой.

Опыт покажет, что деревянная линейка — тело из диэлектрика — притягивается к заряженным телам подобно телу из проводящего материала. Однако если тело из диэлектрика разделить в электрическом поле на две части, то каждая из частей окажется нейтральной. В диэлектрике, помещенном в электрическое поле, заряды не разделяются, следовательно, в нем нет свободных зарядов. Притяжение незаряженного тела из диэлектрика к заряженному телу объясняется тем, что в электрическом поле происходит поляризация диэлектрика, т. е. смещение в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества.

При отсутствии электрического поля электронное облако расположено симметрично относительно атомного ядра (рис. 115), а в электрическом поле с напряженностью Е оно изменяет свою форму, и центр отрицательно заряженного электронного облака уже не совпадает с центром положительного атомного ядра (рис. 116).

В результате поляризации на поверхности вещества появляются связанные заряды (рис. 117). Эти заряды обусловливают взаимодействие нейтральных тел из диэлектрика с заряженными телами. Вектор напряженности a элек трического поля, создаваемого связанными зарядами на поверхности диэлектрика, направлен внутри диэлектрика противоположно вектору напряженности , внешнего электрического поля, вызывающего поляризацию (рис. 118). Напряженность электрического поля внутри диэлектрика оказывается равной , или

Физическая величина, равная отношению модуля напряженности электрического поля в вакууме к модулю напряженности электрического поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества:

Поляризация - процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве. Поляризация диэлектриков — явление, связанное с поляризацией связанных зарядов в диэлектрике и поворотом электрических диполей под воздействием внешнего электрического поля. Поляризацию диэлектриков характеризует вектор электрической поляризации.

В зависимости от механизма поляризации, поляризацию диэлектриков можно подразделить на следующие типы:

Электронная — смещение электронных оболочек атомов под действием внешнего электрического поля. Самая быстрая поляризация (до 10-15 с). Не связана с потерями.

Ионная — смещение узлов кристаллической структуры под действием внешнего электрического поля, причем смещение на величину, меньшую, чем величина постоянной решетки. Время протекания 10-13 с, без потерь.

Дипольная (Ориентационная) — протекает с потерями на преодоление сил связи и внутреннего трения. Связана с ориентацией диполей во внешнем электрическом поле.

Электронно-релаксационная — ориентация дефектных электронов во внешнем электрическом поле.

Ионно-релаксационная — смещение ионов, слабо закрепленных в узлах кристаллической структуры, либо находящихся в междоузлие.

Структурная — ориентация примесей и неоднородных макроскопических включений в диэлектрике. Самый медленный тип.

Самопроизвольная (спонтанная) — благодаря наличию этого типа поляризации в диэлектрике проявляются нелинейность свойств, то есть явление гистерезиса. Отличается очень высокими значениями диэлектрической проницаемости (от 900 до 7500 у некоторых видов конденсаторной керамики). Введение спонтанной поляризации, как правило, увеличивает тангенс угла потерь материала (до 10-2)

Резонансная — ориентация частиц, собственные частоты которых совпадают с частотами внешнего электрического поля.

10. Применение т. Гаусса для расчета электростатического поля некоторых заряженных тел.

q=_V∫ρdV, (1) ρ – объемная плотность заряда.

q=_S∫σdS, (2) σ – поверхностная плотность заряда.

q=_l∫τdl, (3) τ – линейная плотность заряда.

~Ed~S=En*dS=E*cosφ*dS, En – проекция.

_S∫En*dS=(1/ε₀)* _V∫ρdV

I). Бесконечная равномерно заряженная плоскость (т.е. σ не зависит от поверхности, которую мы имеем).

_S∫En*dS=(1/ε₀)* _S1∫ σ dS1, dS=dS1, dS1 – площадка самой поверхности.

Вектор напряженности всегда перпенд-н поверхности заряда.

E_┴=E1=E2=E

E_║=0, E1+E2=2E, 2E*_S∫dS=(σ /ε₀)* _S1∫dS1, 2E*S= σ*S/ε0

E= σ/(2ε0) (5)

Для конечной поверхности в курсе общей физики рассматриваются расстояния << размера поверхности. В этом случае ф-ла (5) применима.

D – параметр характеризующий размер плоскости.

1). r<<D – формула (5) справедлива для точек далеких от края поверхности.

2). r>>D – в этом случае в данной точке считают напряженность для точечного заряда.

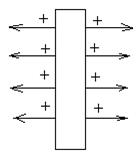
II). Напряженность электростатического поля двух бесконечных разноименно заряженных плоскостей.

~E1=-~E2. В силу электростатической индукции под действием электростатического поля 1-й плоскости во 2-й плоскости произойдет перераспределение зарядов. После обрывания заземления на 2-й плоскости отрицательные заряды.

~E2=-~E2’, ~E2+~E2’=0, ~E1=-~E1’, ~E1+~E1’=0, ~E2+~E1’=~E

E=σ/(2ε0)+σ/(2ε0)=σ/ε0 (6)

Эл. поле м/у двумя пластинами будет определяться ф-лой (6). Если рассматриваемые пластины конечны, но расстояние м/у пластинами d<<D, то расчет электрического поля ведется по ф-ле (6).

Для любых точек пространства, расстояние до которых много больше размеров плоскостей (r>>D>>d), эл. поле = 0.

(самостоятельно)

…

…

III). Поле бесконечного заряженного цилиндра.

R – радиус цилиндра, l – длина цилиндра, l→∞, l>>R.

τ=dq/dl – линейная плотность заряда.

Окружим данный цилиндр коаксиальной цилиндрической поверхностью (цилиндры явл-ся коаксиальными если их центры совпадают).

E_┴=E, E_||=0.

_S∫En*dS=(1/ε₀)* _l1∫τ*dl₁, En – проекция на нормаль поверхности; угол м/у нормалью будет составлять 0⁰.

E~1/r², _S∫E*cos0*dS=E*S=E*2πrl, _l∫τ*dl=τ*l, E*2πrl=τ*l/ε0

E(r)=τ/2πrε0 (7), r>=R.

При r=R – максимальная напряженность.

При r<R – напряженность = 0.

IV). Напряженность поля равномерно заряженной сферы.

τ=dq/dS=const, q=τ*S=4πr²τ

Теорема Гаусса: _S∫En*dS=(1/ε₀)* _S1∫τ dS1,

_S∫En*dS=_S∫E*cos0*dS=|E~1/r²|=E*_S∫dS=E*S=4πr²E

(1/ε0)*_S1∫τ*dS1=τ*S1/ε0=4πR²τ/ε0=q/ε0

E*4πR²=q/ε0,

E=q/4πR²ε0 (8)

Ф-ла (8) справедлива если r>=R.

r=R=>E=(1/4πε)*4πR²τ/R²=τ/ε

E=τ/ε – напряженность эл. поля огранич-го двумя пл-ми.
11. Поведение векторов E и D на границе раздела двух диэлектриков.

.

Запишем теорему Гауса для цил. (тк в ди-ке нет свободных электронов)

, т.е нормальная компанента поля 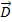уменьшается не прерывно

Плоский контур:

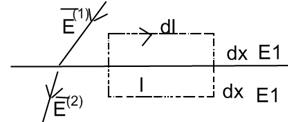
Для поля 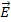справедливо условие потенциальности: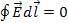

=0

касательная компанента поля 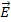изменяется непрерывно. Отметим что рез-т справедлив также и для границ раздела диэлектрик-метал, или метал-метал

Дата добавления: 2015-10-21