
Читайте также:
|
Подмножество рёбер двудольного графа называется паросочетанием, если никакие два ребра из паросочетания не имеют общей вершины. Паросочетание в двудольном графе с максимальным количеством рёбер в нём называется максимальным (или полным), если никакое другое паросочетангие на этом граф не содержит рёбер больше, чем максимальное. Паросочетания с меньшим количеством рёбер, чем полное, называются частичными.
Теорема Холла: паросочетание будет максимальным, если любые k вершин из меньшей доли вершин, мощностью n  , будут иметь рёбра в совокупности по меньшей мере с k вершинами из большей доли вершин, мощностью n
, будут иметь рёбра в совокупности по меньшей мере с k вершинами из большей доли вершин, мощностью n  , где 1<=k<= n
, где 1<=k<= n  и n
и n  <= n
<= n  .
.
Существует несколько алгоритмов нахождения совершенного паросочетания. Рассмотрим точный алгоритм, использующий так называемые чередующиеся цепи. Вершина в двудольном графе будет называться парной, если она является концом одного из рёбер паросочетания. Цепь, соединяющая две непарные вершины, в которой чередуются рёбра, входящие и не входящие в паросочетание, называется чередующейся. Чередующаяся цепь всегда имеет нечётную длину (в том числе и единицу).
Имея чередующуюся цепь, можно на одно ребро увеличить паросочетание, удалив из него рёбра, входящие в чередующуюся цепь и добавив рёбра из чередующейся цепи, которые не входили в паросочетание. Если длина чередующейся цепи равна единице, то просто добавляем это ребро в паросочетание. Паросочетание будет максимальным тогда и только тогда, когда не будет существовать чередующейся цепи относительно него.
В более простом эвристическом алгоритме нахождения максимального паросочетания на каждом этапе выбирается вершина минимальной степени и в пару к ней берётся из другой доли вершина тоже минимально возможной степени. После чего полученная пара удаляется из двудольного графа вместе со всеми своим рёбрами и процесс повторяется для следующей пары вершин.
Двудольный граф задаётся своей, так сказать, прямоугольной «четвертью», поскольку две из остальных «четвертей» полностью нулевые, а последняя совпадает с первой. Строки этой «четверти» соответствуют вершинам одной доли, а столбцы – вершинам другой доли.
В цепи Маркова имеется n состояний, квадратная матрица P переходов размером n, и вектор x длины n, определяющий начальное состояние цепи. Каждый элемент P  матрицы перехода равен вероятности перехода цепи из i-о состояния в j-е за единицу времени. Если в матрице перехода P все положительные (не нулевые) значения заменить единицами, то получим матрицу смежности A ассоциированного с этой цепью Маркова орграфа.
матрицы перехода равен вероятности перехода цепи из i-о состояния в j-е за единицу времени. Если в матрице перехода P все положительные (не нулевые) значения заменить единицами, то получим матрицу смежности A ассоциированного с этой цепью Маркова орграфа.
Из i-о состояния в j-е можно попасть тогда и только тогда, когда в ассоциированном орграфе цепи Маркова существует орцепь, соединяющая соответствующие этим состояниям вершины, и наименьшее возможное время попадания равно длине кратчайшей из таких орцепей.
Цепь Маркова, в которой из любого состояния можно попасть в любое другое (ассоциированный орграф сильно связан), называется неприводимой. Состояния бывают возвратные и невозвратные. В возвратные состояния цепь Маркова возвращается независимо от продолжительности процесса, а в невозвратные цепь попадает несколько раз и более не возвращается. Состояние возвратно тогда и только тогда, когда существование из соответствующей ему вершины ассоциированного орграфа орцепи в какую-то другую вершину влечёт за собой существование обратной орцепи.
Кроме того, состояния бывают периодические и не периодические. Состояние будет периодическим с периодом t (t>1), если в состояние можно вернуться по истечении времени, кратного t. Состояние будет периодическим тогда и только тогда, когда в ассоциированном орграфе длина каждой орцепи, проходящей через соответствующую этому состоянию вершину, кратна t.
Состояние цепи Маркова называется эргодическим, если оно возвратно и не периодично. Если все состояния являются эргодическими, то это эргодическая цепь Маркова.
Задания по теореме Холла и цепям Маркова
| И. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е
 
|
| А. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е Ж
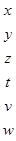 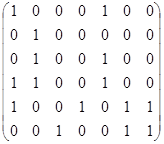
|
| Ю. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. Что можно сказать о состояниях цепи Маркова, если её ассоциированный орграф является турниром? |
| Ь. | За круглым столом n человек играют в кости. При нечётном числе очков кость переходит к соседу слева, при двух или четырёх очках – соседу справа, а при шести – остаётся на месте и бросается вновь. Доказать, что цепь Маркова, соответствующая игре, эргодична. |
| G. | Как меняются условия теоремы Холла для двудольного графа с несколькими компонентами связности. |
| Н. | «Задача о гареме». Пусть каждый юноша желает взять в жёны более чем одну знакомую девушку. Найти условия существования решения для этой задачи. (Заменить каждого юношу несколькими экземплярами и применить теорему Холла). |
| Э. | Что можно сказать о состояниях цепи Маркова, если её ассоциированный орграф является гамильтоновым орграфом (существует орцикл со всеми вершинами орграфа)? |
| Ф. | В задаче о пьянице существует условие: из одного кабачка его выгоняют сразу и он оказывается в соседней с этим кабачком точке. Как это условие отразиться на классификации состояний? А если то же самое происходит в обоих кабачках? |
| Я. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. В транзитивном турнире существование дуг (w,v) и (v,u) влечёт за собой существование дуги (w,u). Что можно сказать о состояниях цепи Маркова, если её ассоциированный орграф является транзитивным турниром? |
| Р. | Найти условия существования частичного паросочетания, если условия теоремы Холла не выполнены. Определить максимальное число юношей, которые могут жениться на знакомых им девушках. |
| Ъ. | Как можно построить бесконечную цепь Маркова? Построить бесконечную цепь, в которой каждое состояние невозвратно. |
| Ч. | Доказать, что регулярный двудольный граф (у всех вершин одинаковые степени) обладает совершенным паросочетанием. |
| Ц. | Доказать, что если P и Q матрицы перехода цепей Маркова, то P  Q тоже матрица перехода. Что можно сказать об орграфах, ассоциированных с P, Q и P Q тоже матрица перехода. Что можно сказать об орграфах, ассоциированных с P, Q и P  Q. Q.
|
| Х. | Сформулируйте задачу о двумерном случайном блуждании и классифицируйте состояния соответствующей цепи Маркова. |
| О. | Пусть выполнены условия теоремы Холла и каждый из m юношей знаком по меньшей мере с t девушками, t  m. Доказать индукцией по m, что супружеские пары могут быть составлены по крайней мере t! способами. m. Доказать индукцией по m, что супружеские пары могут быть составлены по крайней мере t! способами.
|
| П. | Пусть выполнены условия теоремы Холла и каждый из m юношей знаком по меньшей мере с t девушками, t>m. Доказать индукцией по m, что супружеские пары могут быть составлены по крайней мере t! /(t-m)! способами. |
| Ы. | Доказать, что любая конечная цепь Маркова имеет по меньшей мере одно возвратное состояние. Доказать, что если конечная цепь Маркова неприводима, то каждое её состояние возвратно. |
| Т. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д
 
|
| Б. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е Ж
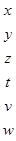 
|
| У. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания
А Б В Г Д
 
|
| Е. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е Ж
 
|
| Г. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д
 
|
| В. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е Ж
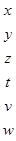 
|
| Ж. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е Ж
 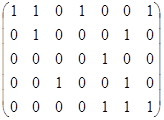
|
| М. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е
 
|
| S. | Сколько существует совершенных паросочетаний в полном двудольном графе с n1 и n2 вершинами в долях (K 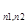 )? )?
|
| Л. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е
 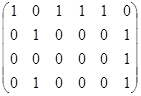
|
| Д. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е
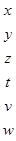 
|
| К. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д Е
 
|
| С. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д
 
|
| З. | С помощью чередующихся цепей и метода последовательного исключения пар с минимальными степенями найти в двудольном графе все максимальные паросочетания.
А Б В Г Д
 
|
Планарность и теорема Эйлера
Операция подразбиения ребра состоит в установке на этом ребре (в середине) новой вершины. Таким образом, вместо одного старого ребра появляются два новых, и появляется дополнительно новая вершина степени два. Граф называется подразбиением другого графа, если его можно получить из этого другого графа путём последовательного применения операции подразбиения рёбер. Подразбиение графа имеет по сравнению с самим графам больше вершин и больше рёбер. Увеличение числа вершин в подразбиении графа происходит только за счёт вершин степени два.
Графы называются гомеоморфными, если существуют их подразбиения, являющиеся изоморфными.
Плоским называется граф, изображённый на плоскости так, что никакие два его ребра (или, вернее, представляющие их кривые) геометрически не пересекаются нигде, кроме вершины, являющейся общим концом для этих рёбер. Граф, изоморфный плоскому, называется планарным.
Теорема: графа K 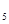 и K
и K  не планарны. Значит, любой граф, содержащий K
не планарны. Значит, любой граф, содержащий K 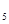 и K
и K  в качестве подграфа, не планарен. Оказывается, что K
в качестве подграфа, не планарен. Оказывается, что K 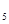 и K
и K  - это по существу единственные не планарные графы в том смысле, что любой не планарный граф содержит один из них. Теорема Куратовского: граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K
- это по существу единственные не планарные графы в том смысле, что любой не планарный граф содержит один из них. Теорема Куратовского: граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K 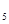 или K
или K  .
.
Плоский граф разбивает плоскость, на которой он изображён, на грани, окружённые рёбрами графа. Одна грань у графа всегда не ограничена, она называется бесконечной. Теорема Эйлера: для связного плоского графа n+f=m+2, где f – число граней у графа. У дерева, например, f=1 (одна бесконечная грань). Для не связных плоских графов теорема Эйлера имеет вид: n+f=m+p+1, где p – число компонент связности.
Следствие теоремы Эйлера: для связного планарного графа с n>=3 вершинами m<=3  n-6. Отсюда получаем, что K
n-6. Отсюда получаем, что K 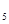 не планарен, так как для него 3
не планарен, так как для него 3  n-6=9, а m=10.
n-6=9, а m=10.
В K  каждая грань ограничена по крайней мере четырьмя рёбрами, так как циклы в двудольном графе имеют чётную длину. Значит, каждая грань приносит как минимум 4 ребра, при этом каждое ребро посчитали дважды (каждое ребро разделяет две грани). 4
каждая грань ограничена по крайней мере четырьмя рёбрами, так как циклы в двудольном графе имеют чётную длину. Значит, каждая грань приносит как минимум 4 ребра, при этом каждое ребро посчитали дважды (каждое ребро разделяет две грани). 4  f<=2
f<=2  m. По теореме Эйлера для плоского связного графа f=m+2-n. Значит, 4
m. По теореме Эйлера для плоского связного графа f=m+2-n. Значит, 4  (m+2-n)<=2
(m+2-n)<=2  m. Отсюда 2
m. Отсюда 2  m<=4
m<=4  n-8 или 18<=16, противоречие. Значит, K
n-8 или 18<=16, противоречие. Значит, K  не планарен.
не планарен.
Теорема, в любом планарном графе существует вершина, степень которой не больше 5. Доказываем от противного. Считаем граф плоским, связным и n>=3. Если степень каждой вершины не менее 6, то каждая вершина приносит по меньшей мере 6 рёбер, при этом каждое ребро посчитали дважды. Получили: 6  n<=2
n<=2  m. Но по теореме Эйлера m<=3
m. Но по теореме Эйлера m<=3  n-6, то есть получили 6
n-6, то есть получили 6  n<=6
n<=6  n-12, противоречие.
n-12, противоречие.
Толщина графа t – это наименьшее число планарных графов, объединение (наложение) которых даёт граф. Толщина графа t является мерой его не планарности. Толщина планарного графа равна 1, а толщина K 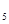 и K
и K  - двум. Оценка снизу для толщины графа t получается из теоремы Эйлера. Часто эта оценка является истинным значением толщины. t>={m/(3
- двум. Оценка снизу для толщины графа t получается из теоремы Эйлера. Часто эта оценка является истинным значением толщины. t>={m/(3  n-6)} t>=[(m+3
n-6)} t>=[(m+3  n-7)/(3
n-7)/(3  n-6)], где [x] и {x} – целые числа и [x]<=x<={x} и {x}=-[-x].
n-6)], где [x] и {x} – целые числа и [x]<=x<={x} и {x}=-[-x].
Задания по планарности и теореме Эйлера
| Ж. | Построить граф с 6 вершинами и 12 рёбрами, содержащий одновременно подграфы, гомеоморфные K 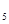 и K и K  . Два графа гомеомерфны, если они могут быть получены из одного и того же графа «включением в его рёбра» новых вершин степени 2. . Два графа гомеомерфны, если они могут быть получены из одного и того же графа «включением в его рёбра» новых вершин степени 2.
|
| Д. | Граф B 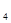 - это регулярный граф с 16 вершинами и 32 рёбрами. Все вершины имеют степень 4. Он представляет собой два куба (24 ребра), причём соответствующие вершины кубов соединены рёбрами (ещё 8 рёбер). Планарен ли граф B - это регулярный граф с 16 вершинами и 32 рёбрами. Все вершины имеют степень 4. Он представляет собой два куба (24 ребра), причём соответствующие вершины кубов соединены рёбрами (ещё 8 рёбер). Планарен ли граф B 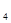 ? ?
|
| Н. | Проверьте теорему Эйлера для а) колеса с n вершинами (W  ); б) платоновых графов: тетраэдра (K ); б) платоновых графов: тетраэдра (K 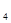 ), куба, октаэдра, додекаэдра; в) графа, образованного вершинами, рёбрами и гранями шахматной доски размером n ), куба, октаэдра, додекаэдра; в) графа, образованного вершинами, рёбрами и гранями шахматной доски размером n  n; г) полного двудольного графа с 2 и n вершинами в долях (K n; г) полного двудольного графа с 2 и n вершинами в долях (K  ). ).
|
| А. | Три соседа пользуются тремя колодцами (с водой, маслом и повидлом). Чтобы не встречаться, они хотят проложить непересекающиеся дорожки от каждого дома к каждому колодцу. Выполнимо ли это? |
| Б. | Граф G  c n вершинами, в котором вершины v c n вершинами, в котором вершины v  и v и v  смежны тогда и только тогда, когда числа i и j взаимно просты (не имеют общих делителей). При каких n графы G смежны тогда и только тогда, когда числа i и j взаимно просты (не имеют общих делителей). При каких n графы G  планарны? планарны?
|
| В. | Докажите, что граф Петерсена не планарен.

|
| М. | Существует ли планарный граф без петель и кратных рёбер, у которого а) 7 вершин и 16 рёбер; б) 8 вершин и 17 рёбер? |
| Р. | Пусть G – граф, с числом граней, меньшим 12. Доказать, что если степень любой вершины G не меньше трёх, то в G существует грань, ограниченная самое большее четырьмя рёбрами. |
| С. | Доказать, что если граф содержит не менее 11 вершин, то он сам и его дополнение одновременно не могут быть планарны. Это верно и для 9 вершин (без доказательства). Построить граф с 8 вершинами так, чтобы и он сам и его дополнение были планарны. Дополнение графа – вершины те же, а рёбра только те, которых нет в самом графе. |
| Т. | Какое наибольшее число граней может быть у 5-вершинного графа? Изобразите его. |
| У. | Существует ли 6-вершинный граф, у которого 9 граней? Построить все попарно неизоморфные 6-вершинные графы, имеющие 8 граней. |
| Х. | Доказать, что в каждом планарном графе без петель и кратных рёбер есть вершина степени не большей, чем 5. |
| Ф. | Графы G  и G и G  имеют 6 вершин и одинаковое число граней. У G имеют 6 вершин и одинаковое число граней. У G  4 вершины степени 4 и 2 вершины степени 3. У G 4 вершины степени 4 и 2 вершины степени 3. У G  2 вершины степени 5, а остальные вершины имеют степень, меньше 5. Какие степени могут быть у остальных вершин G 2 вершины степени 5, а остальные вершины имеют степень, меньше 5. Какие степени могут быть у остальных вершин G  ? Изобразить все G ? Изобразить все G  и G и G  . .
|
| Ц. | Граф, все грани которого треугольники, называется триангуляцией. Доказать, что триангуляция с n>2 вершинами имеет 3  n-6 рёбер и 2 n-6 рёбер и 2  n-4 граней. n-4 граней.
|
| Ч. | Доказать, что если у графа каждый простой цикл содержит не менее k рёбер (k>2), то m<(k  (n-2)/(k-2)) +1. m – число рёбер в графе. (n-2)/(k-2)) +1. m – число рёбер в графе.
|
| Ъ. | Доказать, что в любом планарном графе, имеющим не менее 4 вершин, найдутся хотя бы 4 вершины, степени которых не больше 5. |
| Ы. | Граф называется k-связным, если при удалении (k-1) его вершин получается связный граф. Доказать, что 6-связных планарных графов (без петель и кратных рёбер) не существует. |
| Ь. | Доказать, что кубический граф (степени всех вершин равны 3), граница каждой грани которого имеет не менее 5 вершин, содержит по крайней мере 20 вершин. Привести пример такого графа. |
| Э. | Пусть для кубического графа (степени всех вершин равны 3) f  (i>2) – число граней с i рёбрами. Доказать, что (i>2) – число граней с i рёбрами. Доказать, что  (6-i) (6-i)  f f  =12. =12.
|
| Ю. | Толщина графа – минимальное число планарных графов, объединение которых даёт граф. Найти толщину графа Петерсена.

|
| Я. | Толщина графа – минимальное число планарных графов, объединение которых даёт граф. Доказать, что всякий непланарный граф гомеоморфен некоторому графу толщины 2. Два графа гомеомерфны, если они могут быть получены из одного и того же графа «включением в его рёбра» новых вершин степени 2. |
| S. | Толщина графа – минимальное число планарных графов, объединение которых даёт граф. Доказать, что для полного графа с n вершинами (K  ) его толщина t(K ) его толщина t(K  ) )  [(n+7)/6], где [x] – целая часть x. Доказать, что при n<9 имеет место равенство, а при n=9 и n=10 – строго неравенство. [(n+7)/6], где [x] – целая часть x. Доказать, что при n<9 имеет место равенство, а при n=9 и n=10 – строго неравенство.
|
| О. | У графа 4 грани. Перерисуйте граф 4 раза так, чтобы бесконечной гранью стала по очереди каждая грань.

|
| К. | Какое наименьшее число вершин надо удалить из графов, чтобы получились планарные графы: а) граф Петерсена
 б)
б)

|
| Л. | Какое наименьшее число рёбер надо удалить из графов, чтобы получились планарные графы: а) граф Петерсена
 б) K
б) K  ; в) B ; в) B  . Граф B . Граф B  - это регулярный граф с 16 вершинами и 32 рёбрами. Все вершины имеют степень 4. Он представляет собой два куба (24 ребра), причём соответствующие вершины кубов соединены рёбрами (ещё 8 рёбер). - это регулярный граф с 16 вершинами и 32 рёбрами. Все вершины имеют степень 4. Он представляет собой два куба (24 ребра), причём соответствующие вершины кубов соединены рёбрами (ещё 8 рёбер).
|
| Е. | При каких n графы планарны? А)
n «секций», каждая «секция» – полный граф K  . Получится 2 . Получится 2  (n+1) вершин 4 крайних вершины имеют степень 3, а остальные – степень 5.
Б) то же, как и в А), только две крайние вершины соединены ребром. Итого, из четырёх крайних вершин 2 имеют теперь степень 4. (n+1) вершин 4 крайних вершины имеют степень 3, а остальные – степень 5.
Б) то же, как и в А), только две крайние вершины соединены ребром. Итого, из четырёх крайних вершин 2 имеют теперь степень 4.
|
| З. | Построить все попарно неизоморфные не планарные графы без петель и кратных рёбер, содержащие 6 вершин и 11 рёбер. |
| G. | Рёберный граф L(G) графа G имеет столько вершин, сколько рёбер у графа G (n  =m =m  ). Вершины в L(G) смежны тогда и только тогда, когда соответствующие им рёбра смежны в G. Доказать, что если G не планарен, то и L(G) не планарен. Если G планарен, всегда ли L(G) планарен? ). Вершины в L(G) смежны тогда и только тогда, когда соответствующие им рёбра смежны в G. Доказать, что если G не планарен, то и L(G) не планарен. Если G планарен, всегда ли L(G) планарен?
|
| И. | Построить однородный (регулярный, все степени вершин равны) 9-вершинный граф без петель и кратных рёбер, который не планарен вместе со своим дополнением. Дополнение графа – вершины те же, а рёбра только те, которых нет в самом графе. |
| П. | Пусть G – граф многогранника, все грани которого ограничены пятиугольниками и шестиугольниками. Что можно сказать о числе пятиугольников? Доказать, что если в каждой вершине сходится точно три грани, то число пятиугольников равно 12. |
| Г. | Планарны ли эти графы:



|
Литература
1. Новиков Ф.А. Дискретная математика для программистов – С.-П.:Питер, 2002
2. Андерсен Джеймс. Дискретная математика и комбинаторика – М., С.-П., К.: Издательский дом «Вильямс», 2004
3. Нефедов В.Н., Осипова В.А. Курс дискретной математики – М.: Изд-во МАИ, 1992
4. Уилсон Р. Введение в теорию графов – М.: Мир, 1977
5. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера – М.: Энергоатомиздат, 1988
Дата добавления: 2015-10-13; просмотров: 470 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задания по деревьям и двудольным графам | | | Обучите Членов Команды процедурам по охране труда |