
|
Читайте также: |
Цепь в псевдографе называется эйлеровой, если она проходит по одному разу через каждое ребро. Цикл в псевдографе называется эйлеровым, если он проходит по одному разу через каждое ребро. Граф с эйлеровым циклом называется эйлеровым. В эйлеровом графе существуют и несколько эйлеровых цепей, так как эйлеров цикл можно разбить и на эйлеровы цепи. Граф с эйлеровой цепью, но без эйлерова цикла, называется полуэйлеровым. В полуэйлеровом графе может быть и несколько эйлеровых цепей. Все остальные графы называются не эйлеровыми.
В эйлеровом графе все степени вершин должны быть чётными, а в полуэйлеровом должны быть ровно две вершины нечётной степени. Эйлерова цепь в полуэйлеровом графе начинается и заканчивается в вершинах нечётной степени.
Аналогично орграфам, для графов существует матрица смежности A. Матрицей смежности A графа называется симметричная квадратная матрица порядка n, в которой каждый элемент A 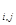 =1, если i-я и j-я вершины связаны ребром (смежны), и A
=1, если i-я и j-я вершины связаны ребром (смежны), и A 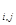 =0, если i-я и j-я вершины не смежны. Сумма элементов матрицы A равна 2
=0, если i-я и j-я вершины не смежны. Сумма элементов матрицы A равна 2  m – удвоенному числу рёбер в графе. Сумма элементов по каждой строке матрицы A равна сумме элементов по соответствующему столбцу матрицы и равна степени соответствующей этой строке вершины графа. По матрице смежности A графа можно проверять условия существования эйлеровых цепей и циклов в графах.
m – удвоенному числу рёбер в графе. Сумма элементов по каждой строке матрицы A равна сумме элементов по соответствующему столбцу матрицы и равна степени соответствующей этой строке вершины графа. По матрице смежности A графа можно проверять условия существования эйлеровых цепей и циклов в графах.
Эйлеровы цепи и циклы можно строить по рисунку графа и его по матрице смежности A. Возьмём, например, матрицу смежности A= 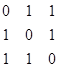 . Степени всех трёх вершин чётны – равны двум. В графе с такой матрицей смежности существует эйлеров цикл. Берём любой не нулевой элемент матрицы, например A
. Степени всех трёх вершин чётны – равны двум. В графе с такой матрицей смежности существует эйлеров цикл. Берём любой не нулевой элемент матрицы, например A  и уменьшаем его и симметричный ему элемент A
и уменьшаем его и симметричный ему элемент A 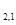 на единицу. Матрица принимает после этого вид:
на единицу. Матрица принимает после этого вид: 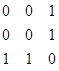 , а в эйлеровом цикле теперь две вершины: 1 и 2, и находимся мы во второй вершине. Находим во второй строке не нулевой элемент – это A
, а в эйлеровом цикле теперь две вершины: 1 и 2, и находимся мы во второй вершине. Находим во второй строке не нулевой элемент – это A  , и повторяем процедуру. Матрица принимает вид:
, и повторяем процедуру. Матрица принимает вид: 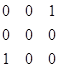 , а в эйлеровом цикле теперь три вершины: 1, 2 и 3, и находимся мы в третьей вершине. Находим в третьей строке не нулевой элемент – это A
, а в эйлеровом цикле теперь три вершины: 1, 2 и 3, и находимся мы в третьей вершине. Находим в третьей строке не нулевой элемент – это A  , и повторяем процедуру. После чего матрица обнуляется полностью, а мы получаем эйлеров цикл: 1, 2, 3, 1.
, и повторяем процедуру. После чего матрица обнуляется полностью, а мы получаем эйлеров цикл: 1, 2, 3, 1.
При построении эйлеровой цепи в качестве начальной вершины надо брать вершину с нечётной степенью. Возьмём, например, матрицу смежности A=  . В графе с такой матрицей смежности ровно две вершины нечётной степени – это первая и третья, и это полуэйлеров граф. В качестве начальной вершины берём любую из двух, например третью. Находим в третьей строке не нулевой элемент и обнуляем его и симметричный ему относительно главной диагонали элемент. Матрица принимает вид:
. В графе с такой матрицей смежности ровно две вершины нечётной степени – это первая и третья, и это полуэйлеров граф. В качестве начальной вершины берём любую из двух, например третью. Находим в третьей строке не нулевой элемент и обнуляем его и симметричный ему относительно главной диагонали элемент. Матрица принимает вид:  и в эйлеровой цепи теперь две вершины: 3 и 2. Повторяем процедуру для второй строки, после чего матрица полностью обнуляется, а мы получаем эйлерову цепь: 3, 2 и 1.
и в эйлеровой цепи теперь две вершины: 3 и 2. Повторяем процедуру для второй строки, после чего матрица полностью обнуляется, а мы получаем эйлерову цепь: 3, 2 и 1.
Эйлеровыми могут быть и псевдогрфы. Возьмём, например, матрицу смежности A= 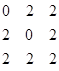 . Степени всех трёх вершин чётны. Начнём строить эйлеров цикл с первой вершины и через четыре шага построения получим матрицу
. Степени всех трёх вершин чётны. Начнём строить эйлеров цикл с первой вершины и через четыре шага построения получим матрицу 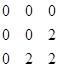 и пять вершин в эйлеровом цикле: 1, 2, 1, 3, 1. Матрица ещё не обнулилась, а в первой строке, где мы находимся, уже нет не нулевых элементов. Находим строку с не нулевыми элементами и строим из соответствующей этой строке вершины маршрут, который затем вставим в эйлеров цикл: 2, 3, 3, 2. Находясь в третьей вершине, мы прошли петлю. Итого, эйлеров цикл имеет вид: 1, 2, 3, 3, 2, 1, 3, 1 и встроенный маршрут выделен в нём жирным шрифтом.
и пять вершин в эйлеровом цикле: 1, 2, 1, 3, 1. Матрица ещё не обнулилась, а в первой строке, где мы находимся, уже нет не нулевых элементов. Находим строку с не нулевыми элементами и строим из соответствующей этой строке вершины маршрут, который затем вставим в эйлеров цикл: 2, 3, 3, 2. Находясь в третьей вершине, мы прошли петлю. Итого, эйлеров цикл имеет вид: 1, 2, 3, 3, 2, 1, 3, 1 и встроенный маршрут выделен в нём жирным шрифтом.
Сильно связный орграф будет эйлеровым, если в нём для каждой вершины полустепень исхода равна полустепени захода. Сильно связный орграф будет полуэйлеровым, если в нём для всех вершин, кроме двух, полустепень исхода равна полустепени захода, в одной из двух оставшихся вершин есть одна лишняя исходящая дуга, а в другой – одна лишняя заходящая дуга.
Эйлеровы цепи и циклы можно строить по рисунку орграфа и его по матрице смежности A. Возьмём, например, матрицу смежности A= 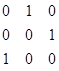 . Для всех трёх вершин полустепени исхода совпадают с полустепенями захода. В орграфе с такой матрицей смежности существует эйлеров цикл. Берём любой не нулевой элемент матрицы, например A
. Для всех трёх вершин полустепени исхода совпадают с полустепенями захода. В орграфе с такой матрицей смежности существует эйлеров цикл. Берём любой не нулевой элемент матрицы, например A  и уменьшаем его на единицу. Матрица принимает после этого вид:
и уменьшаем его на единицу. Матрица принимает после этого вид:  , а в эйлеровом цикле теперь две вершины: 1 и 2, и находимся мы во второй вершине. Находим во второй строке не нулевой элемент – это A
, а в эйлеровом цикле теперь две вершины: 1 и 2, и находимся мы во второй вершине. Находим во второй строке не нулевой элемент – это A  , и повторяем процедуру. Матрица принимает вид:
, и повторяем процедуру. Матрица принимает вид: 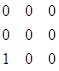 , а в эйлеровом цикле теперь три вершины: 1, 2 и 3, и находимся мы в третьей вершине. Находим в третьей строке не нулевой элемент – это A
, а в эйлеровом цикле теперь три вершины: 1, 2 и 3, и находимся мы в третьей вершине. Находим в третьей строке не нулевой элемент – это A  , и повторяем процедуру. После чего матрица обнуляется полностью, а мы получаем эйлеров цикл: 1, 2, 3, 1.
, и повторяем процедуру. После чего матрица обнуляется полностью, а мы получаем эйлеров цикл: 1, 2, 3, 1.
Эйлерову цепь в орграфе надо начинать строить из вершины, имеющей лишнюю выходящую дугу
Цепь в псевдографе называется гамильтоновой, если она проходит по одному разу через каждую вершину. Цикл в псевдографе называется гамильтоновым, если он проходит по одному разу через каждую вершину. Граф с гамильтоновым циклом называется гамильтоновым. В гамильтоновом графе существуют и несколько гамильтоновых цепей, так как гамильтонов цикл можно разбить и на гамильтоновы цепи. Граф с гамильтоновой цепью, но без гамильтонова цикла, называется полугамильтоновым. В полугамильтоновом графе может быть и несколько гамильтоновых цепей. Все остальные графы называются не гамильтоновыми.
Для нахождения всех гамильтоновых цепей и циклов можно использовать метод, аналогичный методу ветвей и границ. Возьмём граф с матрицей смежности:  . Дерево строим из первой вершины.
. Дерево строим из первой вершины.
6-----4-----5-----1 Гам. цикл 1
5 Х
3-----4-----6 Х
3-----6-----1 Гам. цикл 2
2-----5-----4-----6-----3 Гам. цепь
2-----5-----4 Гам. цепь
3-----4-----5-----2-----1 Гам. цикл 2
5-----2-----3 Гам. цепь
6-----4-----3-----2-----5-----1 Гам. цикл 3
6-----3-----2-----1 Гам. цикл 1
6-----4 Гам. цепь
2-----3-----4-----6-----1 Гам. цикл 3
1-----5-----4-----3-----2 Х
Дерево ветвления строим так, чтобы на каждой его ветви были только уникальные вершины, за исключением седьмой, совпадающей с начальной, первой вершиной, с целью обозначить гамильтонов цикл в графе. Корень (здесь первая вершина)– это нулевой уровень. Из первой вершины есть выход во вторую, шестую и пятую. Первый уровень состоит из этих трёх вершин. Из второй есть выход в 1, 3 и 5, но в первой мы уже были, остаются только 3 и 5. Аналогично, из 6 – в 3 и 4, а из 5 – в 4 и 2. Второй уровень состоит из 6 вершин: 3, 5, 3, 4, 2, 4. и так далее.
Получили три гамильтоновых цикла, каждый цикл получили два раза: в одну сторону и в другую. Если будем строить дерево из другой вершины, например пятой, то получим те же три гамильтоновых цикла. Получили 4 гамильтоновых цепи из первой вершины, две из них кончаются в третьей вершине, а две – в четвёртой. Если будем строить гамильтоновы цепи из третьей вершины, то получим две такие цепи, кончающиеся в первой вершине. Если из третьей вершины будут ещё получены гамильтоновы цепи, то они обязательно закончатся не в первой вершине.
Получили три «безнадёжных» ветви, они помечены буквой «Х». Все они имеют длину пять и из последней пятой вершины есть выходы только в уже пройденные этой веткой вершины.
С помощью дерева ветвления строят и минимальные пути из одной вершины в другую. Дерево строят постепенно, по уровням, пока не появится конечная искомая вершина. Простые пути максимальной длины тоже определяются с помощью дерева ветвления. Максимальная длина простого пути равна n-1, поэтому для этой задачи дерево ветвления строят до максимально возможного уровня. Дерево ветвления можно использовать и для орграфов.
Платоновы графы – это регулярные графы, образованные вершинами и рёбрами пяти правильных многогранников – платоновых тел: тетраэдра (K 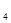 ), куба, октаэдра, додекаэдра и икосаэдра.
), куба, октаэдра, додекаэдра и икосаэдра.
Задания по маршрутам и путям
| З. | Для каких чисел n1, n2 и n следующие графы являются эйлеровыми: а) полный граф с n вершинами (K 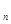 ); б) полный двудольный граф с n1 и n2 вершинами в долях (K ); б) полный двудольный граф с n1 и n2 вершинами в долях (K 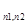 ); в) колесо с n вершинами (W ); в) колесо с n вершинами (W 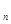 ). Есть ли среди платоновых графов (тетраэдра (K ). Есть ли среди платоновых графов (тетраэдра (K 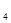 ), куба, октаэдра, додекаэдра) эйлеровы? ), куба, октаэдра, додекаэдра) эйлеровы?
|
| У. | Девять гурманов проводят каждый вечер в ресторане в течении n дней. Они всегда сидят за круглым столом, причём любые двое из них являются соседями только один раз. Чему равно n? Рассмотреть полный граф на 9 вершинах (K 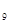 ), в нём n замкнутых циклов без общих рёбер. ), в нём n замкнутых циклов без общих рёбер.
|
| Ф. | Есть ли в орграфе эйлеровы цепи или циклы, гамильтоновы цепи или циклы? Перечислить все, если есть.
| |||
| Ъ. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе простые пути максимальной длины. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
| |||
| Е. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти минимальный путь и простую цепь максимальной длины из первой вершины в седьмую. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| В. | Доказать, что в сильно связном орграфе с симметричной матрицей смежности существует контур, проходящий по одному разу через каждую дугу орграфа. |
| К. | Докажите, что граф Петерсена не является гамильтоновым. Будет ли он полугамильтоновым? Если да, то сколько существует в нём гамильтоновых цепей?

|
| Г. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти минимальный путь и простую цепь максимальной длины из первой вершины в седьмую. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| Д. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти минимальный путь и простую цепь максимальной длины из первой вершины в седьмую. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| Т. | Что можно сказать о графах, являющихся одновременно и эйлеровыми и гамильтоновыми? А полуэйлеровыми и полугамильтоновыми, эйлеровыми и полугамильтоновыми, полуэйлеровыми и гамильтоновыми,? Привести примеры. |
| Щ. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе простые пути максимальной длины. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| И. | Для каких чисел n1, n2 и n следующие графы являются гамильтоновыми: а) полный граф с n вершинами (K  ); б) полный двудольный граф с n1 и n2 вершинами в долях (K ); б) полный двудольный граф с n1 и n2 вершинами в долях (K 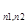 ); в) колесо с n вершинами (W ); в) колесо с n вершинами (W  ). Показать, что все платоновы графы (тетраэдр (K ). Показать, что все платоновы графы (тетраэдр (K 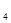 ), куб, октаэдр, додекаэдр) гамильтоновы. ), куб, октаэдр, додекаэдр) гамильтоновы.
|
| О. | Можно ли ходом шахматного коня обойти доску 8  8 так, чтобы каждый ход (двойка клеток) встречался ровно 1 раз? Двойка клеток проходится 1 раз любым из двух возможных способов. А для доски 7 8 так, чтобы каждый ход (двойка клеток) встречался ровно 1 раз? Двойка клеток проходится 1 раз любым из двух возможных способов. А для доски 7  7? Ответ дать в терминах теории графов. 7? Ответ дать в терминах теории графов.
|
| Ш. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе простые пути максимальной длины. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| П. | Можно ли ходом короля обойти шахматную доску 8  8 так, чтобы каждый ход (упорядоченная двойка клеток) встречался ровно 1 раз? А для доски 7 8 так, чтобы каждый ход (упорядоченная двойка клеток) встречался ровно 1 раз? А для доски 7  7? Ответ дать в терминах теории графов. 7? Ответ дать в терминах теории графов.
|
| М. | Может ли король побывать на каждой клетке шахматной доски 8  8 ровно 1 раз и возвратиться в начальную точку? А для доски 7 8 ровно 1 раз и возвратиться в начальную точку? А для доски 7  7? Ответ дать в терминах теории графов. 7? Ответ дать в терминах теории графов.
|
| Л. | Может ли шахматный конь побывать на каждой клетке доски 8  8 ровно 1 раз и возвратиться в начальную точку? А для доски 7 8 ровно 1 раз и возвратиться в начальную точку? А для доски 7  7? Ответ дать в терминах теории графов. 7? Ответ дать в терминах теории графов.
|
| G. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе простые пути максимальной длины. Для проверки нарисовать орграф с матрицей смежности:
в
из 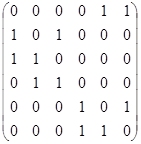 . .
|
| S. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе простые пути максимальной длины. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| Б. | Существуют ли в мультиграфе, заданном матрицей смежности, эйлеровы цепи и циклы? Если да, то найти их. Для проверки нарисовать мультиграф:
в
из 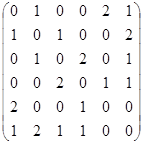 . .
|
| Ы. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе простые пути максимальной длины. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| Ч. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе простые пути максимальной длины. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| Я. | Найти в орграфе эйлеровы цепи и циклы, если они там есть. С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе гамильтоновы цепи и циклы, если они там есть. Для проверки нарисовать орграф с матрицей смежности:
в
из 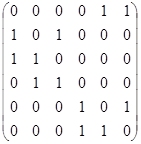 . .
|
| Ц. | Найти гамильтоновы и эйлеровы цепи и циклы в графах:
 
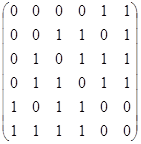
|
| А. | Существуют ли в мультиграфе, заданном матрицей смежности, эйлеровы цепи и циклы? Если да, то найти их. Для проверки нарисовать мультиграф:
в
из 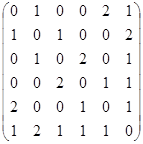
|
| С. | Можно ли ходом ладьи обойти шахматную доску 8  8 так, чтобы каждый ход (упорядоченная двойка клеток) встречался ровно 1 раз? А для доски 7 8 так, чтобы каждый ход (упорядоченная двойка клеток) встречался ровно 1 раз? А для доски 7  7? Ответ дать в терминах теории графов. 7? Ответ дать в терминах теории графов.
|
| Ж. | Найти все эйлеровы цепи и циклы в графе. Сколько их 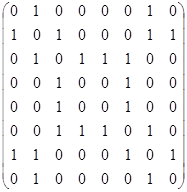 ? ?
|
| Х. | Есть ли в орграфе эйлеровы цепи или циклы, гамильтоновы цепи или циклы? Перечислить все, если есть.
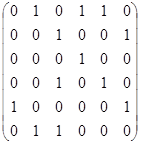 . .
|
| Ю. | Найти в орграфе эйлеровы цепи и циклы, если они там есть. С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе гамильтоновы цепи и циклы, если они там есть. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| Ь. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе простые пути максимальной длины. Для проверки нарисовать орграф с матрицей смежности:
в
из  . .
|
| Н. | Может ли ладья побывать на каждой клетке шахматной доски 8  8ровно 1 раз и возвратиться в начальную точку? А для доски 7 8ровно 1 раз и возвратиться в начальную точку? А для доски 7  7? Ответ дать в терминах теории графов. 7? Ответ дать в терминах теории графов.
|
| Э. | С использованием латинских матриц или метода, аналогичного методу ветвей и границ, найти в орграфе простые пути максимальной длины. Для проверки нарисовать орграф с матрицей смежности:
в
из 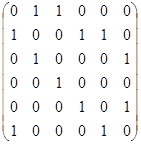 . .
|
Дата добавления: 2015-10-13; просмотров: 332 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Составитель: доц., канд. тех. наук Л.Е.Захарова | | | Деревья и двудольные графы |