
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Московский государственный институт электроники и математики
(Технический университет)
Кафедра «Вычислительные
системы и сети»
Методические указания к самостоятельным и семинарским занятиям по теории графов
Москва 2006
Составитель: доц., канд. тех. наук Л.Е.Захарова
УДК 519.1
Предназначены для решения задач по теории графов как при самостоятельном изучении теории графов, так и при решении задач на семинарах по теории графов в курсе дискретной математики студентами I (дневного) и II (вечернего) курсов специальности 22.0101.
Теория графов: Метод. указания к самостоятельным и семинарским занятиям по теории графов/ Моск. Гос. ин-т электроники и математики; Сост. Л.Е. Захарова. М., 2006. 30 с.
Ил. 3. Библиогр.: 5 назв.
Графы: основные понятия
Граф – это совокупность не пустого множества точек V, называемых вершинами, и множества X отрезков прямых, соединяющих вершины и называемых рёбрами. N 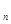 - это граф с n вершинами и без рёбер, или, другими словами, это n изолированных вершин. Ребро графа называется петлёй, если оба конца его являются одной и той же вершиной. Рёбра называются кратными, если концы у них совпадают. Петли тоже могут быть кратными.
- это граф с n вершинами и без рёбер, или, другими словами, это n изолированных вершин. Ребро графа называется петлёй, если оба конца его являются одной и той же вершиной. Рёбра называются кратными, если концы у них совпадают. Петли тоже могут быть кратными.
В псевдографе могут быть и кратные рёбра и петли. В мультиграфе могут быть только кратные рёбра. В графе, если это не оговаривается особо, нет ни петель, ни кратных рёбер.
Вершины графа называются смежными, если их соединяет ребро. Ребра графа смежны, если имеют общую вершину. Степенью вершины является число рёбер, для которых эта вершина является концом. Если степень вершины единица, то вершина называется висячей. Каждая петля увеличивает степень вершины на два.
Для графов приняты следующие обозначения: n – это число вершин в графе (n  0), а m – это число рёбер в нём. В каждом псевдографе (мультиграфе, графе) сумма степеней всех вершин в нём равна 2
0), а m – это число рёбер в нём. В каждом псевдографе (мультиграфе, графе) сумма степеней всех вершин в нём равна 2 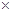 m, так как вклад каждого ребра в эту сумму равен двойке.
m, так как вклад каждого ребра в эту сумму равен двойке.
Изоморфные графы отличаются друг от друга только нумерацией вершин. Изоморфный граф – это тот же самый граф, только по-другому нарисованный. В изоморфных графах числа вершин и рёбер и набор степеней вершин совпадают, но не наоборот. Например, существует два разных графа с n=5, m=6 и набором степеней вершин: 2 2 2 3 3, в одном вершины степени три смежны (имеют общее ребро), а в другом нет.
Маршрут в псевдографе – это последовательность, в которой чередуются вершины и рёбра, их соединяющие. Если нет кратных рёбер, то маршрут можно составить из одних вершин. Число рёбер в маршруте называется его длиной. Незамкнутый маршрут, в котором все рёбра различны, называется цепью. Цепь, в которой все вершины различны, называется простой цепью. Ребро – это простая цепь длиной единица.
Замкнутый маршрут, в котором все рёбра различны, называется циклом. Цикл, в котором все вершины различны, называется простым циклом. Петля – это простой цикл длины единица. Кратные рёбра образуют простой цикл длины два.
Если степени всех вершин графа больше единицы, то в графе существует хотя бы один цикл. Берём любую вершину, из неё выходят как минимум два ребра, выходим из этой вершины по любому из рёбер и попадаем в следующую вершину. У этой новой вершины степень как минимум два, выходим из неё по ребру, не совпадающему с тем, по которому в неё попали. Опять попадаем в новую вершину и так же выходим из неё по новому ребру. Поскольку число вершин в графе конечно, то рано или поздно попадём в вершину, в которой уже были, не обязательно это будет вершина, из которой мы начали маршрут, и получим цикл.
Подграфом графа называется граф, все вершины и рёбра которого содержатся среди вершин и рёбер графа. Подграф называется собственным, если он отличен от самого графа.
Псевдограф называется связным, если для каждой пары его вершин существует маршрут, их соединяющий. Компонентой связности графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа графа. Число компонент связности у графа обозначается переменной p. У связного графа p=1, у N 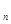 (графа с n изолированными вершинами) p=n.
(графа с n изолированными вершинами) p=n.
Лес – это граф без циклов. Дерево – это связный граф без циклов. Лес, таким образом, состоит из p деревьев. Полный граф содержит все возможные рёбра между n вершинами и обозначается K 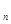 . Число рёбер у полного графа равно m=n
. Число рёбер у полного графа равно m=n 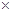 (n-1)/2. В дереве m=n-1, а в лесе m=n-p, так как каждое дерево леса отнимает единицу от числа вершин n.
(n-1)/2. В дереве m=n-1, а в лесе m=n-p, так как каждое дерево леса отнимает единицу от числа вершин n.
В двудольном графе вершины разделяются на две доли (n=n1+n2), а рёбра существуют только между вершинами из разных долей. Двудольный граф может быть полным и не полным. В полном двудольном графе, которой обозначается K 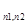 , существуют все возможные ребра между вершинами из разных долей. Число рёбер в полном двудольном графе равно n1
, существуют все возможные ребра между вершинами из разных долей. Число рёбер в полном двудольном графе равно n1 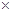 n2.
n2.
Граф называется регулярным (или однородным) если все вершины в нём имеют одну и ту же степень. Если из графа удалить вершину вместе с ребрами, для которых она является концом, то получим подграф графа. Вершина графа называется разделяющей, если её удаление увеличивает количество компонент связности.
Задания по графам
| Н. | Доказать, что если в графе без петель и кратных ребер min степеней вершин не меньше (n-1)/2, то граф связен. Доказывать от обратного: посчитать max числа вершин и их max степень в двух компонентах связности. |
| Ю. | Доказать, что если в псевдографе существует ровно 2 вершины нечётной степени, то существует цепь, соединяющая их. |
| У. | Дополнение графа – это граф с те ми же вершинами, но с рёбрами, которых нет в самом графе. Имеем граф без петель и кратных рёбер и его дополнение. Доказать, а) что хотя бы один из этих графов связен; б) если в графе более 4-х вершин, то хотя бы в одном из графа и его дополнения есть цикл. (Дерево – граф без циклов, у него m=n-1). |
| Р. | Доказать, что в связном псевдографе две простые цепи максимальной длины имеют хотя бы одну общую вершину. Верно ли, что у них всегда есть общее ребро. |
| Э. | Пусть у графа без петель и кратных рёбер n вершин и p компонент связности. Доказать, что m (число рёбер) (n-p)  m m  (n-p) (n-p) 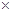 (n-p+1)/2. (Для нижней оценки рассмотреть лес из p деревьев, а для верхней – (p-1) изолированную вершину и полный граф с (n-p+1) вершинами.) Вывести отсюда, что если у n-вершинного графа (n>1) m>(n-2) (n-p+1)/2. (Для нижней оценки рассмотреть лес из p деревьев, а для верхней – (p-1) изолированную вершину и полный граф с (n-p+1) вершинами.) Вывести отсюда, что если у n-вершинного графа (n>1) m>(n-2) 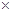 (n-1)/2, то он связен (p=1) (n-1)/2, то он связен (p=1)
|
| Т. | Доказать, что если в мультиграфе степень каждой вершины больше единицы, то в нём есть цикл. А в псевдографе? |
| И. | Выяснить, какие наборы степеней вершин могут быть у 6-вершинных связных графов без петель и кратных рёбер, имеющих 7 рёбер и содержащих вершину степени два и вершину степени три. Для каждого допустимого набора степеней вершин построить пример соответствующего графа. |
| Ь. | Сколько существует попарно неизоморфных графов без петель и кратных рёбер, в которых: а) n=6 m=11; б) n=7 m=18; в) n=8 m=24. |
| П. | Доказать, что если из связного мультиграфа удалить произвольное ребро, содержащееся в некотором цикле, то новый мультиграф будет также связен. А псевдограф и граф? |
| G. | Известно, что 6-вершинные графы G и H не имеют петель и кратных рёбер, двусвязны (граф k-связен, если при удалении любых (k-1) вершин получается связный граф), содержат по 10 рёбер и степень одной вершины в каждом из них равна d1 (1  d1 d1  5), а степени всех остальных вершин – d2 (d2<d1). Доказать, что графы H и G изоморфны. 5), а степени всех остальных вершин – d2 (d2<d1). Доказать, что графы H и G изоморфны.
|
| М. | Доказать, что в мультиграфе всякий замкнутый маршрут нечётной длины l (l>2) содержит простой цикл. Справедливо ли аналогичное утверждения для маршрутов чётной длины? |
| Д. | Изобразить все попарно неизоморфные 6-вершинные графы без петель и кратных рёбер, состоящие а) из 4 компонент; б) из 3 компонент; в) из одной компоненты и имеющие 7 рёбер и ровно 2 висячие вершины. |
| Ц. | Граф (без петель и кратных рёбер) называется самодополнительным, если он изоморфен своему дополнению. Дополнение графа – это граф с те ми же вершинами, но с рёбрами, которых нет в самом графе. Показать, что число вершин в самодополнительном графе либо кратно четырем (равно 4 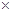 z, z>0) либо равно 4 z, z>0) либо равно 4 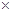 z+1 (z>-1). z+1 (z>-1).
|
| Ш. | Сколько существует попарно неизоморфных графов без петель и кратных рёбер, в которых: а) n=6 m=7 и p=2 (p – число компонент связности); б) n=8 и сумма степеней всех вершин >52? |
| Ж. | Сколько существует попарно неизоморфных, не имеющих петель и кратных рёбер, кубических (все вершины степени 3) графов с 6 вершинами? c 8? |
| К. | Показать, что в любом графе без петель и кратных рёбер, содержащем не менее 2 вершин, найдутся как минимум 2 вершины с одинаковыми степенями. |
| С. | Доказать, что всякий связный псевдограф, имеющий не менее двух вершин, содержит вершину, не являющуюся разделяющей. Висячие вершины в графе – не разделяющие. Если их в графе нет, то удалять из циклов рёбра до тех пор, пока они не появятся. |
| Ч. | Граф (без петель и кратных рёбер) называется самодополнительным, если он изоморфен своему дополнению. Дополнение графа – это граф с те ми же вершинами, но с рёбрами, которых нет в самом графе. Доказать, что среди 4-вершинных графов самодополнительным является один, а среди 5-вершинных – два. |
| Г. | Построить все попарно неизоморфные 5-вершинные графы, не имеющие петель, кратных рёбер и изолированных вершин. |
| Ъ. | Граф (без петель и кратных рёбер) называется самодополнительным, если он изоморфен своему дополнению. Дополнение графа – это граф с те ми же вершинами, но с рёбрами, которых нет в самом графе. Доказать, что самодополнительный граф связен. |
| Е. | Сколько существует попарно неизоморфных 6-вершинных графов без петель и кратных рёбер с набором степеней вершин: 2, 2, 3, 3, 3, 5? |
| Л. | Доказать, что 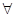 n>2 n>2  n-вершинный связный граф без петель и кратных рёбер, содержащий (n-1) вершин с неравными друг другу степенями. n-вершинный связный граф без петель и кратных рёбер, содержащий (n-1) вершин с неравными друг другу степенями.
|
| Б. | nj – число вершин степени j в графе. Построить все попарно неизоморфные графы без петель и кратных рёбер, у которых: а) n2=1 n3=n4=2 (n=5); б) n2=3 n3=2 n4=1 (n=6). |
| Х. | Вершина называется разделяющей, если после её удаления в графе увеличивается число компонент связности. Доказать, что если вершина является разделяющей в графе, то она не является разделяющей в дополнении графа. Дополнение графа – это граф с те ми же вершинами, но с рёбрами, которых нет в самом графе. |
| О. | Индукцией по n доказать, что связный псевдограф с n вершинами содержит не менее (n-1) рёбер (n>0). |
| Ы. | Граф называется самодополнительным, если он изоморфен своему дополнению. Дополнение графа – это граф с те ми же вершинами, но с рёбрами, которых нет в самом графе. Расстояние между вершинами – это длина кратчайшей цепи, соединяющей их. Диаметр графа – это max расстояний в нём. Доказать, что диаметр самодополнительного графа не меньше 2 и не больше 3. |
| S. | Известно, что графы G и H не имеют петель и кратных рёбер, двусвязны (граф k-связен, если при удалении любых (k-1) вершин получается связный граф), содержат 6 вершин и 8 рёбер каждый. У графа G имеется 2 вершины степени 2, а у H – 4 степени 3. Изоморфны ли G и H? |
| Ф. | Дополнение графа – это граф с те ми же вершинами, но с рёбрами, которых нет в самом графе. Расстояние между вершинами – это длина кратчайшей цепи, соединяющей их. Диаметр графа – это max расстояний в нём. Доказать, что если граф несвязен, или его диаметр не меньше 3, то диаметр дополнения графа не больше 3. |
| Я. | В двудольном графе вершины разделяются на две доли (n=n1+n2), а рёбра существуют только между вершинами из разных долей. Доказать, что если в двудольном графе без кратных рёбер m>((n-1)/2)  и n>1, то граф связен. Доказывать от обратного, посчитать для p=2 число рёбер в двух полных двудольных графах. и n>1, то граф связен. Доказывать от обратного, посчитать для p=2 число рёбер в двух полных двудольных графах.
|
| З. | Существует ли 6-вершинный граф без петель и кратных рёбер с набором степеней вершин: 2, 2, 2, 4, 5, 5? |
| В. | Изобразить все попарно неизоморфные 4-вершинные графы без петель и кратных рёбер. |
Орграфы: основные понятия
Орграфы – это ориентированные или направленные графы. В орграфе вершины соединяются дугами, причём одна вершина называется началом, а другая концом дуги. Дуга исходит из своего начала и заходит в свой конец. Дуга орграфа называется петлёй, если её начало и конец являются одной и той же вершиной. Дуги называются кратными, если начала и концы у них совпадают. Петли тоже могут быть кратными. Две дуги орграфа составляют симметричную пару дуг, если начало одной из них является концом другой и наоборот.
Аналогично графам, в орпсевдографе могут быть и кратные дуги и петли. В ормультиграфе могут быть только кратные дуги. В орграфе, если это не оговаривается особо, нет ни петель, ни кратных дуг.
Вершины орграфа называются смежными, если их соединяет дуга. Полустепенью исхода вершины является число дуг, для которых эта вершина является началом. Полустепенью захода вершины является число дуг, для которых эта вершина является концом. Если сумма полустепеней исхода и захода вершины равна единицы, то вершина называется висячей. Каждая петля увеличивает полустепени исхода и захода вершины на единицу.
Для орграфов приняты те же обозначения, что и для графов: n – это число вершин в орграфе (n  0), а m – это число дуг в нём. В каждом орграфе суммы полустепеней исхода и захода всех вершин в нём равны m, так как вклад каждой дуги в каждую из сумм равен единице. Каждая дуга откуда-то исходит и куда-то заходит.
0), а m – это число дуг в нём. В каждом орграфе суммы полустепеней исхода и захода всех вершин в нём равны m, так как вклад каждой дуги в каждую из сумм равен единице. Каждая дуга откуда-то исходит и куда-то заходит.
Изоморфные орграфы тоже отличаются друг от друга только нумерацией вершин. Изоморфный орграф – это тот же самый орграф, только по-другому нарисованный. В изоморфных орграфах числа вершин и рёбер и наборы полустепеней исхода и захода вершин совпадают, но не наоборот.
Путь в орграфе – это последовательность, в которой чередуются вершины и дуги, их соединяющие. Путь может идти только от начала дуги к её концу, против направления дуги путь идти не может. Если нет кратных дуг, то путь можно составить из одних вершин. Число дуг в пути называется его длиной. Незамкнутый путь, в котором все дуги различны, называется цепью. Цепь, в которой все вершины различны, называется простой цепью. Дуга – это простая орцепь длиной единица.
Замкнутый путь, в котором все дуги различны, называется контуром. Контур, в котором все вершины различны, называется простым контуром. Петля – это простой контур длины единица. Симметричная пара дуг образует простой контур длины два.
Если полустепени исхода всех вершин орграфа больше нуля, то в орграфе существует хотя бы один контур. Берём любую вершину, из неё выходит как минимум одна дуга, по этой дуге попадает в следующую вершину пути. Из этой новой вершины тоже исходит как минимум одна дуга, выходим по ней в следующую вершину пути. Опять попадаем в новую вершину и так же выходим из неё по новой дуге. Поскольку число вершин в орграфе конечно, то рано или поздно попадём в вершину, в которой уже были, не обязательно это будет вершина, из которой мы начали путь, и получим контур. Аналогичное рассуждение справедливо и в случае, если полустепени захода всех вершин орграфа больше нуля.
Орподграфом орграфа называется орграф, все вершины и дуги которого содержатся среди вершин и дуг орграфа. Орподграф называется собственным, если он отличен от самого орграфа.
Орграф называется сильно связным, если для каждой пары его вершин существуют пути в обе стороны, их соединяющие. Другими словами, каждая пара вершин сильно связного орграфа входит в контур. Компонентой сильной связности орграфа называется его сильно связный орподграф, не являющийся собственным орподграфом никакого другого сильно связного орподграфа орграфа. Число компонент сильной связности у орграфа тоже обозначается переменной p.
Орграф называется односторонне связным, если для каждой пары его вершин существует соединяющий их путь по крайней мере в одну сторону. Если в орграфе дуги заменить рёбрами, то получим ассоциированный с орграфом граф. Орграф называется слабо связным, если ассоциированный с ним граф является связным.
В полном орграфе для каждой пары вершин существует по крайней мере одна дуга между ними. В полном орграфе могут быть симметричные пары дуг. В турнире для каждой пары вершин существует ровно одна дуга между ними. В турнире не могут быть симметричные пары дуг. Стоком называется вершина полного орграфа или турнира, полустепень исхода которой равна нулю. Истоком называется вершина полного орграфа или турнира, полустепень захода которой равна нулю. В полном орграфе или в турнире могут быть сток, или исток, или и сток и исток, а могут и не быть. В сток можно попасть по дуге из любой вершины полного орграфа или турнира, а из истока можно попасть по дуге в любую вершину полного орграфа или турнира.
Орграф может быть задан своей матрицей смежности A. Матрицей смежности A орграфа называется квадратная матрица порядка n, в которой каждый элемент A 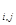 =1, если существует дуга из i-й вершины в j-ю, и A
=1, если существует дуга из i-й вершины в j-ю, и A 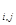 =0, если такой дуги нет. Сумма элементов матрицы A равна m – числу дуг в орграфе. Сумма элементов по каждой строке матрицы A равна полустепени исхода соответствующей этой строке вершины орграфа, а сумма элементов по каждому столбцу матрицы A равна полустепени захода соответствующей этому столбцу вершины орграфа.
=0, если такой дуги нет. Сумма элементов матрицы A равна m – числу дуг в орграфе. Сумма элементов по каждой строке матрицы A равна полустепени исхода соответствующей этой строке вершины орграфа, а сумма элементов по каждому столбцу матрицы A равна полустепени захода соответствующей этому столбцу вершины орграфа.
Контуры в орграфе можно определять как вручную по рисунку орграфа, так и по матрице смежности A орграфа. Все контуры длиной единица (петли) находятся на главной диагонали матрицы смежности A. Все контуры длиной два (симметричные пары дуг) находятся на главной диагонали квадрата матрицы смежности A - A  . И так далее. Все контуры орграфа максимальной длины n находятся на главной диагонали n-й степени матрицы смежности A - A
. И так далее. Все контуры орграфа максимальной длины n находятся на главной диагонали n-й степени матрицы смежности A - A  . Так что при n=4 для определения контуров орграфа надо получить его матрицу смежности, её квадрат, куб и четвёртую степень.
. Так что при n=4 для определения контуров орграфа надо получить его матрицу смежности, её квадрат, куб и четвёртую степень.
Матрицей смежности компоненты сильной связности орграфа является квадратная подматрица матрицы смежности самого орграфа, содержащая только строки и столбцы, соответствующие вершинам этой компоненты сильной связности.
Одна вершина орграфа достижима из другой вершины, если существует орцепь (в том числе и длиной единица – дуга) из этой другой вершины в достижимую из неё вершину. Матрицей достижимости T орграфа называется квадратная матрица порядка n, в которой каждый элемент T 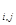 =1, если j-я вершина достижима из i-й вершины, и T
=1, если j-я вершина достижима из i-й вершины, и T 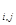 =0 в противном случае. Матрицу достижимости можно получить как вручную из рисунка орграфа, так их из матрицы смежности A орграфа по формуле: T=E
=0 в противном случае. Матрицу достижимости можно получить как вручную из рисунка орграфа, так их из матрицы смежности A орграфа по формуле: T=E  A
A  A
A 
 …
…  A
A  , где E – единичная квадратная матрица порядка n.
, где E – единичная квадратная матрица порядка n.
Матрицей сильной связности S орграфа называется квадратная матрица порядка n, в которой каждый элемент S 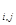 =1, если j-а вершина достижима из i-й вершины и, наоборот, i-а вершина достижима из j-й вершины, и S
=1, если j-а вершина достижима из i-й вершины и, наоборот, i-а вершина достижима из j-й вершины, и S 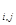 =0 в противном случае. Матрицу сильной связности можно получить как вручную из рисунка орграфа, так их из матрицы достижимости T орграфа по формуле: S=T
=0 в противном случае. Матрицу сильной связности можно получить как вручную из рисунка орграфа, так их из матрицы достижимости T орграфа по формуле: S=T  T
T 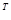 , где
, где  - это поэлементная операция «and», а T
- это поэлементная операция «and», а T 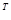 означает операцию транспонирования матрицы T когда строки матрицы становятся её столбцами и наоборот.
означает операцию транспонирования матрицы T когда строки матрицы становятся её столбцами и наоборот.
Задания по орграфам
| Л. | Обратный к G орграф получается из G переменой направления каждой дуги. Приведите пример орграфа G, изоморфного своему обратному. Что можно сказать о матрицах смежности орграфа и обратного к нему орграфа? |
| К. | Доказать, что слабо связный орпсевдограф является сильно связным тогда и только тогда, когда в нём существует ориентированный замкнутый контур, содержащий каждую дугу орпсевдографа хотя бы один раз. |
| Д. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. Построить все попарно неизоморфные турниры с а) 3 вершинами; б) 4 вершинами. Сколько среди них сильно связных, односторонне связных и слабо связных? |
| J. | Доказать, что в n-вершинном (n>1) слабо связном орграфе (без петель и кратных дуг) число дуг (m): (n-1)  m m  (n-1) (n-1) 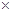 (n-2), если орграф не является сильно связным. (n-2), если орграф не является сильно связным.
|
| О. | Пусть G – слабо связный ориентированный псевдограф, не являющийся односторонним. Доказать, что в G нет такой вершины, удаление которой даёт сильно связный псевдограф. |
| У. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. В транзитивном турнире существование дуг (w,v) и (v,u) влечёт за собой существование дуги (w,u). Показать, что вершины транзитивного турнира можно упорядочить по «силе» (по степени исхода). |
| Ъ. | Определить, имеют ли контуры орграфы с матрицами смежности:
в в
а)из 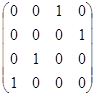 ;б) из ;б) из 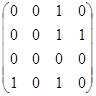 . .
|
| Ф. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. В транзитивном турнире существование дуг (w,v) и (v,u) влечёт за собой существование дуги (w,u). Показать, что транзитивный турнир, имеющий не менее двух вершин, не может быть сильно связным. |
| Н. | Бесконтурным ориентированным мультиграфом называется мультиграф без контуров (ориентированных простых циклов). Доказать, что в нём существует вершина с нулевой полустепенью исхода. |
| Р. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. Доказать, что в турнире не может быть больше одного истока (с нулевой полустепенью захода) и одного стока (с нулевой полустепенью исхода). |
| S. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. Доказать, что если из сильно связного турнира удалить одну вершину, то останется либо сильно связный орграф, либо он же, но без одной дуги. |
| Г. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. Построить все попарно неизоморфные турниры с 5 вершинами, содержащие один исток (с нулевой полустепенью захода) и один сток (с нулевой полустепенью исхода). |
| Ж. | Доказать, что в n-вершинном (n>1) односторонне связном орграфе (без петель и кратных дуг) число дуг (m): (n-1)  m m  (n-1) (n-1)  , если орграф не является сильно связным. , если орграф не является сильно связным.
|
| В. | Изобразить все попарно неизоморфные орграфы, содержащие: а) 3 вершины и хотя бы одну дугу; б) 4 вершины и 4 дуги; в) 5 вершин и 3 дуги. Сколько среди них сильно связных, односторонне связных и слабо связных. |
| З. | Доказать, что если для каждой вершины ориентированного псевдографа полустепень исхода положительна, то в нём существует ориентированный контур (петля – контур длины 1). |
| Х. | Доказать, что если в орграфе отсутствуют вершины с нулевой полустепенью исхода (захода), то в нём есть простой контур. |
| Ц. | Доказать, что удаление из орграфа вершины с полустепенью исхода (захода) не большей единицы, приводит к орграфу, контуры которого совпадают с контурами исходного орграфа. |
| Т. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. Пусть у одной вершины турнира полустепень исхода не меньше, чем полустепень исхода любой другой вершины. Доказать, что расстояние от этой вершины до любой другой вершины турнира не превосходит 2. |
| П. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. Пусть {v  , …,v , …,v 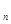 } – множество вершин турнира, а вектор d } – множество вершин турнира, а вектор d  длины n содержит полустепени исхода вершин. Доказать, что длины n содержит полустепени исхода вершин. Доказать, что  (d (d  (v (v  )) ))  = =
 (n – 1 - d (n – 1 - d  (v (v  )) )) 
|
| С. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. Пусть {v  , …,v , …,v 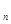 } – множество вершин турнира, а вектора d } – множество вершин турнира, а вектора d  и d и d  длины n содержат полустепени исхода и захода вершин соответственно. Доказать, что а) длины n содержат полустепени исхода и захода вершин соответственно. Доказать, что а)  d d  (v (v  )= )=  d d  (v (v  );
б) );
б)  (d (d  (v (v  )) ))  = =  (d (d  (v (v  )) )) 
|
| И. | Пусть орграф G (без петель и кратных дуг) является по крайней мере слабо связным, {v  , …,v , …,v 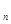 } – множество его вершин (n>1) и вектора d } – множество его вершин (n>1) и вектора d  и d и d  длины n содержат полустепени исхода и захода вершин соответственно. d длины n содержат полустепени исхода и захода вершин соответственно. d  (v (v  ) - d ) - d  (v (v  )=1; d )=1; d  (v (v  ) - d ) - d  (v (v  )= -1; d )= -1; d  (v (v  ) = d ) = d  (v (v  ) для i=3, …, n. Доказать, что в G существует орцепь (v ) для i=3, …, n. Доказать, что в G существует орцепь (v  ,v ,v  ), содержащая все его дуги. ), содержащая все его дуги.
|
| Ш. | Определить матрицы достижимости и сильной связности для орграфов с матрицами смежности:
в в
а) из 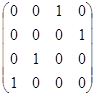 ; б) из ; б) из 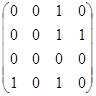 . .
|
| Ы. | Определить матрицы достижимости и сильной связности для орграфов с матрицами смежности:
в в
а)из  ;б) из ;б) из 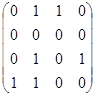 ;
в
в) из ;
в
в) из  . .
|
| Ч. | Определить, имеют ли контуры орграфы с матрицами смежности:
в в
а)из  ;б) из ;б) из 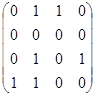 ;
в
в) из ;
в
в) из  . .
|
| Я. | Определить матрицу сильной связности, найти количество компонент сильной связности и определить матрицы смежности этих компонент, построить орграф, заданный матрицей
в
смежности: из  . .
|
| Ю. | Определить матрицу сильной связности, найти количество компонент сильной связности и определить матрицы смежности этих компонент, построить орграф, заданный матрицей
в
смежности: из  . .
|
| Ь. | Определить матрицу сильной связности, найти количество компонент сильной связности и определить матрицы смежности этих компонент, построить орграф, заданный матрицей
в
смежности: из  . .
|
| G. | Орграф полный, если в нём любые две вершины соединены хотя бы одной дугой. Доказать, что во всяком полном ориентированном псевдографе существует источник, т.е. вершина, из которой достижима любая другая вершина псевдографа. |
| Э. | В турнире (полном орграфе) каждая пара вершин связана ровно одной дугой. В транзитивном турнире существование дуг (w,v) и (v,u) влечёт за собой существование дуги (w,u). Показать, что в транзитивном турнире существует единственная орцепь, соединяющая все вершины (полугамильтонова цепь). |
| А. | Изобразить все попарно неизоморфные орграфы (без петель и кратных дуг), содержащие: а) 3 вершины и 3 дуги; б) 3 вершины и 4 дуги; в) 4 вершины и 3 дуги. Сколько среди них сильно связных, односторонне связных и слабо связных. |
| Е. | Доказать, что в n-вершинном (n>2) сильно связном орграфе (без петель и кратных дуг) число дуг (m): n  m m  n n  (n-1). (n-1).
|
| Б. | Изобразить все попарно неизоморфные ориентированные псевдографы, содержащие: а) 2 вершины и 2 дуги; б) 2 вершины и 3 дуги; в) 3 вершины и 2 дуги. Сколько среди них сильно связных, односторонне связных и слабо связных. |
Дата добавления: 2015-10-13; просмотров: 169 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Стиль жизни консультанта Faberlic идеально сочетается с концепцией Wellness | | | Маршруты в графах и пути в орграфах |