| А.
| Доказать, что во всяком дереве с n>1 вершинами содержится не менее 2 висячих вершин.
|
| Б.
| Пусть n1 – число висячих вершин n-вершинного дерева, не содержащего вершин степени 2. Доказать, что n1>n/2.
|
| В.
| Индукцией по n доказать, что каждое дерево с n>1 вершинами является двудольным графом. Какие деревья являются полными двудольными графами?
|
| Г.
| Изобразить все попарно неизоморфные деревья: а) с 6 рёбрами и 3 висячими вершинами; б) с 6 рёбрами и 4 висячими вершинами; в) с 7 рёбрами и 3 висячими вершинами; г) с 8 рёбрами и 3 вершинами степени 3.
|
| Д.
| Подсчитать число попарно неизоморфных 7-вершинных деревьев, у которых сумма квадратов степеней вершин меньше 27.
|
| Е.
| Существуют ли двудольные кубические (регулярные, степени 3) графы? Нарисовать, если да. Может ли быть различным число вершин в долях в регулярном двудольном графе?
|
| П.
| Если графы G и H (без петель и кратных рёбер) изоморфны, то для каждого d>-1 число вершин степени d в графах G и H одинаково. Показать, что а) это условие (подчёркнуто выше) является достаточным для изоморфизма графов с 4 и менее вершинами; б) условие не является достаточным для изоморфизма графов с 5 и более вершинами, причём, если число вершин не менее 6, то даже для деревьев.
|
| Р.
| Описать и нарисовать все графы, являющиеся деревьями вместе со своими дополнениями.
|
| Ж.
| Построить все попарно неизоморфные растущие деревья (в них существует источник с полустепенью захода, равной нулю) с а) 4 вершинами; б) 5 вершинами; в) 6 вершинами, не содержащие ориентированных цепей длины, превосходящей 3.
|
| З.
| Доказать, что слабо связный орграф является растущим деревом (в нём существует источник с полустепенью захода, равной нулю) тогда и только тогда, когда лишь одна его вершина имеет нулевую полустепень захода, а полустепень захода любой из остальных вершин равна 1.
|
| Т.
| Построить дерево по его коду: а) 0010100111; б) 00110101000111; в) 0000010011011111;
г) 01001000110111;
д) 00100010110111;
е) 00010111010000101111.
|
| У.
| По вектору установить, является ли он кодом дерева (если да, то построить дерево): а) 001011; б) 110 0110; в) 001001; г) 010011; д) 00111001; е) 0001100111.
|
| Ф.
| Множество векторов разбить на классы так, чтобы каждый класс состоял из кодов попарно изоморфных деревьев: а) {0100101101, 0101000111, 0001110101, 0101001011, 010001101}; б) {010001011011, 000110011101, 001001011101, 010010010111, 010001100111}; в) {0011010011, 0100110011, 00100110101, 0100101101, 0011001101}.
|
| Х.
| Доказать по индукции, что для каждого дерева в его коде число нулей совпадает с числом единиц, и число единиц среди первых k координат кода (k<2  m) не превосходит числа нулей среди тех же координат. Длина кода дерева равна 2 m) не превосходит числа нулей среди тех же координат. Длина кода дерева равна 2  m, где m – число рёбер в дереве. m, где m – число рёбер в дереве.
|
| Ц.
| Длина кода дерева равна 2  m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: а) f(m)<4 m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: а) f(m)<4 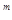 +1; б) f(m)<C +1; б) f(m)<C 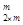 +1; в) f(m)<C +1; в) f(m)<C 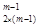 +1. +1.
|
| Ч.
| Длина кода дерева равна 2  m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: f(m)= m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: f(m)=  . f(0)=f(1)=1
(Число Каталана) . f(0)=f(1)=1
(Число Каталана)
|
| Ъ.
| Вершина корневого дерева называется висячей,
если она отлична от корня и имеет степень, равную 1. а) у дерева k висячих вершин и нет вершин степени 2, отличных от корня. Доказать, что при k>1 n<2  k+1; б) пусть степени всех n вершин, кроме корня, не превышают 3, а степень корня не превышает 2. Доказать, что число висячих вершин не больше n/2. k+1; б) пусть степени всех n вершин, кроме корня, не превышают 3, а степень корня не превышает 2. Доказать, что число висячих вершин не больше n/2.
|
| S.
| Диаметр дерева – длина максимальной простой цепи в нём. Доказать, что в дереве с нечётным диаметром любые две простые цепи максимальной длины имеют хотя бы общее ребро. А с чётным?
|
| Я.
| Доказать, что некорневое дерево однозначно с точностью до изоморфизма восстанавливается, если заданы все попарные расстояния между его висячими вершинами.
|
| Ю.
| Расстояние между вершинами – это длина кратчайшей цепи, соединяющей их. Диаметр графа – это max расстояний в нём. а) для каждого d>2 указать граф, диаметр которого равен d, а диаметр любого его связного остовного (содержащего все вершины графа) дерева равен 2  d. d.
|
| Ы.
| Вычислить цикломатическое число а) полного графа с n вершинами (K  ); б) полного двудольного графа с n1 и n2 вершинами в долях (K ); б) полного двудольного графа с n1 и n2 вершинами в долях (K 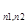 ); в) пустого графа с n вершинами (n изолированных вершин - N ); в) пустого графа с n вершинами (n изолированных вершин - N  ); г) колеса с n вершинами (W ); г) колеса с n вершинами (W  ); д) платоновых графов: тетраэдра (K ); д) платоновых графов: тетраэдра (K 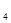 ), куба, октаэдра, додекаэдра; е) графа Петерсена; ж) любого связного регулярного степени r (степени всех вершин равны r) графа с n вершинами. ), куба, октаэдра, додекаэдра; е) графа Петерсена; ж) любого связного регулярного степени r (степени всех вершин равны r) графа с n вершинами.
|
| Ь.
| Остовное дерево графа содержит все вершины графа и некоторые его рёбра. Найти остовное дерево: а) полного графа с 5 вершинами (K 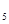 ); б) полного двудольного графа с тремя вершинами в каждой из долей (K ); б) полного двудольного графа с тремя вершинами в каждой из долей (K  ); в) колеса с 5 вершинами (W ); в) колеса с 5 вершинами (W 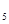 ); г) циклического графа с 6 вершинами (C ); г) циклического графа с 6 вершинами (C  ); д) графа Петерсена; е) платоновых графов: тетраэдра (K ); д) графа Петерсена; е) платоновых графов: тетраэдра (K 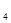 ), куба, октаэдра, додекаэдра. ), куба, октаэдра, додекаэдра.
|
| Э.
| Остовное дерево графа содержит все вершины графа и некоторые его рёбра. Пусть T1 и T2 – остовные деревья графа G. Доказать, что для каждого ребра e из T1 существует ребро f из T2, и если в T1 заменить e на f, то получим опять остовное дерево графа G. Доказать, что T1 можно перевести в T2, меняя по очереди рёбра из T1 на рёбра из T2.
|
| К.
| Приведите примеры (когда это возможно) а) регулярного (степени всех вершин равны) двудольного графа; б) двудольного платонова графа (тетраэдр (K 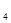 ), куб, октаэдра, додекаэдр); в) бесконечного двудольного графа. ), куб, октаэдра, додекаэдр); в) бесконечного двудольного графа.
|
| Л.
| Что можно сказать о дополнении полного двудольного графа? Дополнение графа – это граф с те ми же вершинами и с рёбрами, которых нет в самом графе. Опишите матрицу смежности двудольного графа. Что можно сказать о матрицах смежности двудольного графа и его дополнения?
|
| О.
| Люди – это вершины, а знакомых людей связывает ребро. Доказать, что среди 6 человек всегда найдутся 3 таких, которые либо все знают друг друга (цикл длины 3), либо ни один из них не знает двух других.
|
| Н.
| G – двудольный граф с наибольшей степенью вершин d. Покажите, что существует двудольный граф G1(v1,v2), в котором v1 и v2 содержат одинаковое число вершин и G1 - регулярный граф степени d, причём G – это подграф G1. Показать алгоритм построения G1 из G.
|
| G.
| Расстояние между вершинами – это длина кратчайшей цепи, соединяющей их. Диаметр графа – это max расстояний в нём. Диаметр дерева – длина максимальной простой цепи в нём. Доказать, что для каждого связного графа существует его остовное дерево, диаметр которого не более чем в два раза превосходит диаметр графа.
|
| С.
| Построить коды деревьев:
|

 m) не превосходит числа нулей среди тех же координат. Длина кода дерева равна 2
m) не превосходит числа нулей среди тех же координат. Длина кода дерева равна 2  m, где m – число рёбер в дереве.
m, где m – число рёбер в дереве.
 m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: а) f(m)<4
m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: а) f(m)<4 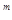 +1; б) f(m)<C
+1; б) f(m)<C 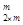 +1; в) f(m)<C
+1; в) f(m)<C 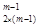 +1.
+1.
 m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: f(m)=
m, где m – число рёбер в дереве. В коде дерева m нулей и m единиц, код начинается с нуля и заканчивается единицей. Пусть f(m) – количество различных кодов деревьев с m рёбрами. Доказать: f(m)=  . f(0)=f(1)=1
(Число Каталана)
. f(0)=f(1)=1
(Число Каталана)
 k+1; б) пусть степени всех n вершин, кроме корня, не превышают 3, а степень корня не превышает 2. Доказать, что число висячих вершин не больше n/2.
k+1; б) пусть степени всех n вершин, кроме корня, не превышают 3, а степень корня не превышает 2. Доказать, что число висячих вершин не больше n/2.
 d.
d.
 ); б) полного двудольного графа с n1 и n2 вершинами в долях (K
); б) полного двудольного графа с n1 и n2 вершинами в долях (K 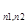 ); в) пустого графа с n вершинами (n изолированных вершин - N
); в) пустого графа с n вершинами (n изолированных вершин - N  ); г) колеса с n вершинами (W
); г) колеса с n вершинами (W  ); д) платоновых графов: тетраэдра (K
); д) платоновых графов: тетраэдра (K 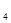 ), куба, октаэдра, додекаэдра; е) графа Петерсена; ж) любого связного регулярного степени r (степени всех вершин равны r) графа с n вершинами.
), куба, октаэдра, додекаэдра; е) графа Петерсена; ж) любого связного регулярного степени r (степени всех вершин равны r) графа с n вершинами.
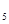 ); б) полного двудольного графа с тремя вершинами в каждой из долей (K
); б) полного двудольного графа с тремя вершинами в каждой из долей (K  ); в) колеса с 5 вершинами (W
); в) колеса с 5 вершинами (W 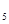 ); г) циклического графа с 6 вершинами (C
); г) циклического графа с 6 вершинами (C  ); д) графа Петерсена; е) платоновых графов: тетраэдра (K
); д) графа Петерсена; е) платоновых графов: тетраэдра (K  ), куба, октаэдра, додекаэдра.
), куба, октаэдра, додекаэдра.
 ), куб, октаэдра, додекаэдр); в) бесконечного двудольного графа.
), куб, октаэдра, додекаэдр); в) бесконечного двудольного графа.