I.Способы задания графов. Степени вершин, матрицы инцидентности и смежности.

Определения

Граф называется d -однородным (d -регулярным), если все его вершины имеют степень d.

Граф на n вершинах называется максимально неоднородным, если среди степеней его вершин присутствуют n -1 различных значений (в этом случае, очевидно, ровно две вершины имеют одинаковые степени, а степени всех остальных вершин различны).

Дополнением графа G=(V,X) называется граф 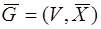, в котором пара вершин v, v' смежна тогда и только тогда, когда она не смежна в G.

Самодополнительным называется граф, изоморфный своему дополнению.

Сильно регулярным с параметрами (d,c,b) называется граф, для которого верны следующие свойства:

­ степени всех вершин совпадают и равны d;

­ для любой пары смежных вершин пересечение их окрестностей состоит из одинакового количества c вершин;

­ для любой пары несмежных вершин пересечение их окрестностей состоит из одинакового количества b вершин.

Вершина графа называется разделяющей (точкой сочленения), если ее удаление из графа увеличивает число компонент связности.

Ребро графа называется мостом (разрезающим ребром), если его удаление из графа увеличивает число компонент связности.

Цикломатическим числом (циклическим порядком) графа называется наименьшее число рёбер, которые надо удалить в графе, чтобы в нём не осталось ни одного цикла.

I.Способы задания графов. Степени вершин, матрицы инцидентности и смежности.

ГР I.1. Построить все попарно не изоморфные графы на n вершинах для n=1,2,3,4,5.

ГР I.2. Доказать, что не существует граф, все степени вершин которого различны.

ГР I.3. Доказать, что максимально неоднородные графы существуют для любого числа вершин.

ГР I.4. Пусть граф G - максимально неоднородный граф на n вершинах, в котором две вершины имеют степень k. Найти взаимосвязь между числами k и n, и доказать, что такой граф однозначно определяется своим вектором степеней.

ГР I.5. Среди графов, построенных в задаче ГР1, найти:

а) все максимально неоднородные;

б) все пары неизоморфных графов, имеющие одинаковые векторы степеней;

в) d -однородные графы.

ГР I.6.

а)описать строение d-однородных графов для d=1 и 2;

б) построить 3-однородные (кубические) графы c числом вершин n≤10.

ГР I.6. Дана матрица инцидентности A_G графа G. Найти матрицу смежности данного графа (вывести зависимость в виде формулы).

ГР I.7. Пусть X - n -множество. Рассмотрим граф G, вершинами которого являются неупорядоченные пары элементов X. Вершины графа считаем смежными, если соответствующие пары элементов множества X имеют непустое пересечение. Найти:

– число вершин графа;

– степени вершин;

число вершин, смежных произвольной паре вершин (выписать вектор пересечений).

ГР I.8. Пусть граф G - сильно регулярный с параметрами (d,c,b). Показать, что граф, дополнительный к G, также сильно регулярный, и найти его параметры (d',c',b').

ГР I.9. Дана матрица инцидентности M_G графа G, столбцы которой линейно независимы. Описать строение графа G.

Дата добавления: 2015-10-13