II. Пути, цепи, циклы, связность.

ГР II.1. Пусть граф G имеет n вершин, m ребер и k компонент связности. Доказать неравенства:

.

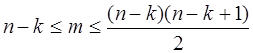ГР II.2. Пусть граф G имеет n вершин и m ребер. Доказать, что если 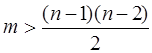, то граф связен.

ГР II.3. Доказать, что если в мультиграфе (графе с кратными ребрами) все вершины имеют степени больше единицы, то в нем есть цикл.

Сформулировать инверсию данного утверждения.

ГР II.4. Доказать, что в мультиграфе любой замкнутый маршрут нечетной длины l ³3 содержит простой цикл. Останется ли утверждение верным для четного l?

ГР II.5. Рассмотрим граф без петель и кратных ребер с n вершинами (n ³2). Доказать, что если степени всех вершин не меньше числа 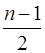, то граф связен. Останется ли утверждение верным, если 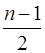заменить на ?

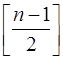ГР II.6. Доказать, что связный граф с n вершинами содержит не менее n -1 ребер.

ГР II.7. Доказать, что вершина v является разделяющей тогда и только тогда, когда существуют непустые непересекающиеся подмножества вершин графа V ₁ и V ₂, такие что для любых вершин v ₁Î V ₁ и v ₂Î V ₂ любой путь из v ₁ в v ₂ содержит v.

ГР II.8. Доказать, что ребро графа является мостом тогда и только тогда, когда оно не входит ни в один цикл графа.

ГР II.9. Доказать, что удаление из графа ребра, являющегося мостом, увеличивает число компонент связности ровно на единицу.

ГР II.10.Доказать, что любой связный граф с числом вершин n³2 содержит вершину, которая не является разделяющей.

ГР II.11. Доказать, что в связном графе любые две простые цепи максимальной длины имеют общую вершину.

ГР II.12. Пусть граф G имеет более 4-х вершин. Доказать, хотя бы один из графов (G либо 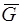) содержит цикл. Построить контрпример для графов с 4-мя вершинами.

ГР II.13. Доказать, что хотя бы один из графов (G или 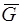) связен.

ГР II.14. Пусть граф G несвязен, или его диаметр не меньше 3. Доказать, что тогда диаметр 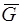не больше 3.

ГР II.15. Пусть вершина v - разделяющая в G. Доказать, что она не является разделяющей в .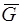

ГР II.16. Пусть граф G - самодополнительный. Найти возможные значения числа его вершин.

ГР II.17. Доказать, что для диаметра D(G) нетривиального самодополнительного графа верны неравенства

2£ D(G) £3.

ГР II.18. Дан граф G, являющийся лесом с n вершинами и m ребрами. Найти число компонент связности G.

ГР II.19. Каково цикломатическое число:

а) дерева

б) простого цикла

в) полного графа K_n?

Дата добавления: 2015-10-13