
|
Читайте также: |
В двудольном граф циклы, если они есть, имеют чётную длину. Дерево – это связный двудольный граф (без циклов, естественно) Если доли вершин двудольного графа перемешаны, то можно по рисунку графа эти доли определить. Надо взять любую вершину и пометить её, как принадлежащую к первой доле (буквой А, например). Тогда все смежные к этой вершине вершины будут из второй доли (буква Б), и, в свою очередь, смежные к вершинам второй доли вершины будут из первой доли, и так далее. Таким же способом можно определять и «двудольность» произвольного графа. Если вершины одной доли смежны, то это не двудольный граф.
Любое дерево может быть задано его двоичным кодом. Код дерева имеет длину 2 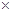 m и состоит из m нулей и m единиц. Для любого начального отрезка кода дерева число единиц в нём не больше числа нулей. Код дерева всегда начинается с 0 и заканчивается 1. Код дерева зависит от того, какую вершину мы выберем в качестве корня. Дерево с одним ребром и двумя вершинами имеет код 01. Каждое ребро дерева имеет в коде свой ноль и свою единицу, причем единица всегда находится в коде далее нуля. Код получается в результат обхода дерева. Обход начинается и заканчивается в корне дерева. Если ребро дерева встречается при обходе первый раз, то в коде появляется 0 этого ребра, а если второй (и последний), то в коде появляется 1 этого ребра. Например, цепочка из 5 вершин (C
m и состоит из m нулей и m единиц. Для любого начального отрезка кода дерева число единиц в нём не больше числа нулей. Код дерева всегда начинается с 0 и заканчивается 1. Код дерева зависит от того, какую вершину мы выберем в качестве корня. Дерево с одним ребром и двумя вершинами имеет код 01. Каждое ребро дерева имеет в коде свой ноль и свою единицу, причем единица всегда находится в коде далее нуля. Код получается в результат обхода дерева. Обход начинается и заканчивается в корне дерева. Если ребро дерева встречается при обходе первый раз, то в коде появляется 0 этого ребра, а если второй (и последний), то в коде появляется 1 этого ребра. Например, цепочка из 5 вершин (C 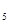 ) является простейшим деревом и имеет код 00001111.
) является простейшим деревом и имеет код 00001111.
Колесо с n вершинами (W 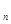 ) имеет одну вершину степени n-1 в центре (ось колеса) и n-1 вершину степени три по окружности колеса. У колеса есть спицы (рёбра, выходящие из оси колеса).. W
) имеет одну вершину степени n-1 в центре (ось колеса) и n-1 вершину степени три по окружности колеса. У колеса есть спицы (рёбра, выходящие из оси колеса).. W 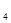 =K
=K 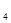 , например, (тетраэдр).
, например, (тетраэдр).
Число Каталана – это число бинарных деревьев с n вершинами. Бинарное дерево с n=0 – это пустое дерево, а с n>0 вершинами – это тройка Д=(Л, К, П), где К – вершина, называемая корнем дерева, Л – левое поддерево с Л вершинами и П – правое поддерево с П вершинами и n=Л+1+П. С  - число различных бинарных деревьев с k вершинами (число Каталана). C
- число различных бинарных деревьев с k вершинами (число Каталана). C  = C
= C  =1 и если 0<=s<=k, то существует C
=1 и если 0<=s<=k, то существует C 
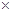 C
C  различных бинарных деревьев вида (s, К, k-1-s). s принимает значения от 0 до k-1, и, значит, С
различных бинарных деревьев вида (s, К, k-1-s). s принимает значения от 0 до k-1, и, значит, С  = C
= C 
 С
С  + C
+ C 
 С
С 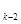 +... + С
+... + С 
 C
C  и k>0. С помощью производящей функции получается, что С
и k>0. С помощью производящей функции получается, что С 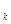 =C
=C  /(k+1).
/(k+1).
Остовное дерево связного графа содержит все его вершины и некоторые рёбра. Для получения остовного дерева в графе находят цикл и убирают из него произвольное ребро. Затем опять находят цикл и убирают ребро, пока циклов в графе не останется. Остовных деревьев может быть несколько. Цикломатическое число  графа – это число рёбер, которые надо удалить из графа, чтобы превратить граф в лес (в дерево, если граф связен).
графа – это число рёбер, которые надо удалить из графа, чтобы превратить граф в лес (в дерево, если граф связен).  =p+m-n. Цикломатическое число леса (и дерева) равно нулю.
=p+m-n. Цикломатическое число леса (и дерева) равно нулю.
Дата добавления: 2015-10-13; просмотров: 207 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Маршруты в графах и пути в орграфах | | | Задания по деревьям и двудольным графам |