Деревья

Лекция 2.3. Деревья. Планарные графы. Реберная и вершинная раскраски графа

Изучаемые вопросы:

Планарные графы. Деревья. Реберная и вершинная раскраски графа. Хроматическое число.

Деревья

Деревья открывали независимо несколько раз Г. Кирхоф, А. Кэли, К. Жордан и по разным поводам.

Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется лесом. Т.о., компонентами леса являются деревья. Лес, состоящий из всех неизоморфных деревьев шестого порядка, изображен на рис 19.

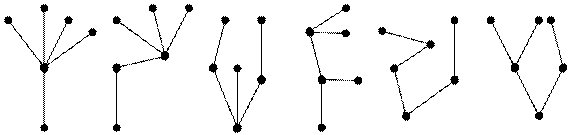
Теорема. Если G – граф с p вершинами и q ребрами, то следующие предложения эквивалентны:

1. G – дерево;

2. G – связный и q=p-1

3. G – не имеет циклов и q=p-1

4. две любые вершины графа G соединяет единственная простая цепь

5. у G нет циклов, но, если какую-либо пару его несмежных вершин соединить ребром, то в полученном графе будет цикл

6. G – связный граф, но при удалении любого ребра получится несвязный граф.

Доказательство. 1) => 2). Т.к. дерево – связный граф без циклов, то по теореме* p-q= 1 => q=p-1

2) => 3). Если граф G – не содержит циклов, то у него ровно p-q компонент по теореме* Однако, p-q= 1, т.е. компонента одна, поэтому G – связный.

3) => 4). Т.к. G – связный, то для любых двух различных вершин A и B существует простая цепь с концами A и B. Если таких цепей имеется две, то их объединение содержит цикл. Однако наличие циклов по теореме* влечет условие k<p-q=1, т.е. компонент нет. Поэтому предположение неверно, и простая цепь – единственная.

4) => 5). Если две различные вершины принадлежат одному циклу, то их можно соединить минимум двумя простыми цепями. Следовательно, у G нет циклов. Если выбрать две несмежные вершины A и B графа G, то существует простая цепь с концами в A и B. Присоединение к G ребра AB дополнит эту цепь до цикла.

5) => 6). Если граф G – несвязный и без циклов, то соединяя ребром две вершины, принадлежащие разным компонентам нельзя получить цикл. Поэтому G – связный и без циклов. Отсюда, удаление любого ребра ведет к несвязности G.

6) => 1). Удаление ребра, принадлежащего циклу, не ведет к несвязности. Поэтому у G нет циклов и это дерево.

Можно выбрать одну из вершин дерева и назвать ее корнем. Само дерево при этом называется корневым. Любое корневое дерево можно ориентировать по направлению от корня к каждой висячей вершине. На рис корнем является вершина A.

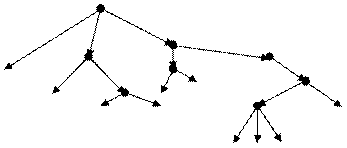
Корневые деревья сильно напоминают родословные и для них можно употреблять «семейную» терминологию: отец, сын, брат и тому подобное. Например, вершина B₃ является отцом для C₃ и C₄, а те, в свою очередь, сыновья для B₃ и братья между собой.

Использование деревьев и такой терминологии может оказаться полезным при решении задач.

Задача. У царя Гвидона было три сына. Из его потомков сто имели по два сына, а остальные умерли бездетными. Сколько потомков было у царя Гвидона?

Решение. Царя Гвидона поместим в корне родословного древа. От него отходят три ветви, соответствующие сыновьям, потом ветви пойдут от сыновей и т.д. При этом в каждую вершину, кроме корневой, входит одна дуга орграфа (стрелка), а выходят либо две, либо не одной. Кроме того, две дуги выходят ровно из ста вершин. Ясно, что число потомков равно именно числу выходящих дуг, т.е. 3+2•100=203.

Дерево можно пометить несколькими способами, однако не все такие способы приводят к неизоморфным деревьям.

Для примера рассмотрим помеченные деревья порядка 4. Непомеченных деревьев порядка 4 всего два вида (рис 21а и 21б).

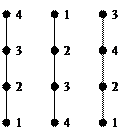
Число способов пометки каждого вида равно числу перестановок вершин, т.е. P₄=4! Однако, при этом возможно получение изоморфных деревьев. Действительно, можно пометить тремя различными способами вершины дерева на рис 21а.

Из рисунка ясно, что второе помеченное дерево является перевернутым первым, т.е. они изоморфны. Но, ни одно из этих деревьев не изоморфно третьему помеченному дереву, т.к. степень вершины с номером 3 у двух первых деревьев равна 2, а у третьего – 1. Поэтому (с учетом переворачивания) помеченных деревьев такого вида будет (4!/2)=12. Другой вид дерева порядка 4 (рис 21б) можно пометить четырьмя различными способами в зависимости от того, какой номер будет присвоен доминирующей (центральной) вершине.

Итого помеченных деревьев порядка 4 оказалось 16=4². Кэли сообщил этот результат на помеченные деревья порядка p.

Теорема Кэли. Для любого p≥3 существует ровно p^p-2 различных помеченных деревьев порядка p.

Планарные графы

Задача (о трех домах и трех колодцах). Имеется три дома и три колодца. Провести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались.

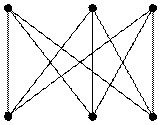
Ранее отмечалось, что возможно несколько изображений одного графа, т.к. все изоморфные графы несут одну и туже информацию. На практике при изготовлении микросхем необходимо выяснить, можно ли схему радиоэлектронного устройства, которая представляет собой граф, изобразить на плоскости без пересечений проводников. Аналогичная задача возникает при проектировании железнодорожных и других путей, где нежелательны переезды.

Т.о. возникает задача построения и исследования плоского графа.

Плоским называется граф, вершины которого являются точками плоскости, а ребра - непрерывные плоскими линиями без самопересечений, причем никакие 2 ребра не имеют общих точек, кроме инцидентной им вершины. Любой граф, изоморфный плоскому, называется планарным.

Все планарные графы укладываются на плоскости (имеют плоскую укладку).

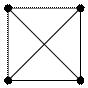
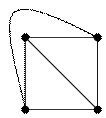
планарный граф плоская укладка

Очевидно, что:

1. Всякий подграф планарного графа планарен.

2. Граф планарен тогда и только тогда, когда каждая связная компонента этого графа – планарный граф.

Гранью плоского графа называется множество всех таких точек плоскости этого графа, которые можно соединить друг с другом плоской кривой, не пересекающей ребра графа.

На рисунке показан плоский граф с четырьмя гранями. Одна из них, неограниченная, называется внешней (4), а остальные внутренними.

Теорема (Эйлер). Для любого плоского связного графа G с p вершинами, q ребрами и r гранями справедливо равенство p – q + r = 2.

Следствие: Если связный простой граф с p (p ≥ 3) вершинами и q ребрами планарен, то имеет место неравенство: q £ 3p – 6.

Следствие: Графы K₅ и K_3,3 не планарны.

Теорема. Почти каждый граф не планарен.

Дата добавления: 2015-10-13