Глава 1. Графы и их применение

Основные понятия теории графов

Пусть дано множество V = {v1, v2,…,vn} и пусть на множестве V определено семейство U = {u1, u2, …, un} пар элементов Uk = {vi, vj}, (k=1, m) произвольной кратности и упорядочения. Пара {V, U} называется графом. Граф, как правило, обозначают прописными латинскими буквами, например G, H. Принято также писать G (V, U) для того, чтобы определить некоторый конкретный граф G.

Элементы v1, v2,…, vn называют вершинами графа, а пары Uк = {vi, vj},

(к = 1, m) – ребрами.

Определению графа можно дать такую интерпретацию. Пусть имеем описание графа:

G (V, U) = {{v1, v2,…, v6}, {{v1, v3}, <v5, v1>, {v3, v4}, <v2, v3>, {v3, v3}}}.

Это описание можно отобразить графически, как показано на рис.3. На этом рисунке некоторые ребра отмечены стрелкой, а соответствующие им пары вершин в описании графа выделены угловыми скобками. Это связано с тем, что для некоторого произвольного ребра можно принимать или не принимать во внимание порядок расположения его концов.

Если этот порядок не существенен, то ребро называется неориентированным, в противном случае ребро называется ориентированным. Ориентированные ребра называются также дугами.

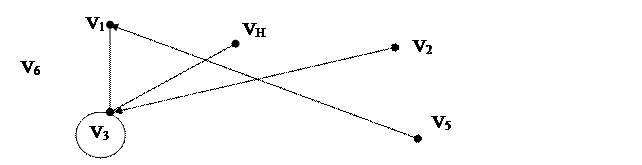
Рис. 3

Для ориентированного ребра определены понятия начальной и конечной вершины. Начальная вершина записывается в начале пары вершин, определяющих дугу, а конечная – в конце. Так, на рис.3 ребра <v5, v1> и <v2, v3> являются дугами. Они представлены упорядоченными парами вершин и в связи с этим обозначены также, как обозначаются упорядоченные множества.

Ребра {v1, v3}, {v3, v4} неориентированы. Для любого неориентированного ребра полагают, что {vi, vj} = {vj, vi}. Ребро {vi, vi} называется петлей. На рис.3 имеем петлю {v3, v3}. Петли обычно неориентированы.

Граф, у которого все ребра неориентированы, называется неориентированным.

Граф, у которого все ребра ориентированы, называется ориентированным или орграфом.

Иногда удобно преобразовывать неориентированный граф в ориентированный – заменой каждого неориентированного ребра парой ориентированных ребер с противоположной ориентацией.

На рис.3 приведен смешанный граф, т.е. содержащий как ориентированные, так и неориентированные ребра и петлю.

Некоторые вершину графа G могут не войти в список пар. Такие вершины называются изолированными. В рассмотренном примере это вершина v6. Граф, у которого все вершины изолированы, называется нуль-графом. Множество ребер такого графа пусто.

Антиподом нуль-графа является полный граф. Ребрами полного графа являются все возможные пары его вершин.

Как в случае ориентированного графа, так и в случае неориентированного, говорят, что ребро инцидентно паре определяющих его вершин.

Одной и той же паре вершин можно поставить в соответствии множество инцидентных ребер. Такие ребра называются кранными. Так, на рис.4 представлены различные пары вершин (vi, vj), инцидентных трем различным ребрам u1, u2, u3. Одно из них направлено, а два – нет.

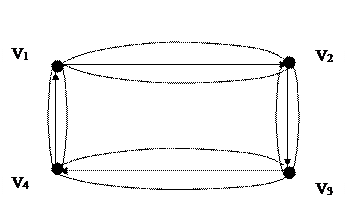
Рис. 4

Граф называется плоским, если он может быть изображен на плоскости так, что все пересечения ребер есть его вершины. Так, граф приведенный на рис.3, плоским не является, а на рис.4 – плоский.

Если граф G представлен конечным множеством ребер, то он называется конечным, независимо от числа вершин. В противном случае - бесконечный.

Граф Н называется частью графа G или частичным графом Н С G, если множество его вершин V (G) графа G и все ребра U являются ребрами G. Частным, но важным типом частичных графов являются подграфы.

Пусть А – подмножество множества вершин V графа G. Подграф G (A) графа G есть такая часть графа, множеством вершин которого является А, а ребрами – все ребра из G, оба конца которых лежат в А.

Для любой части G графа определена дополнительная часть G (дополнение), состоящая из всех тех ребер, которые не принадлежат G, и всех инцидентных им вершин.

Например, граф G на рис.5 неполный. А проведенные недостающие ребра составляют граф дополнение G рис.6.

Рис. 5 Рис. 6

Вершины в графе могут отличаться друг от друга тем, скольким ребрам они принадлежат.

Степенью вершины называется число ребер графа, которым принадлежит эта вершина.

Обозначать степени вершин v1, v2, v3 будем так: δ (v1), δ (v2), δ (v3) и т.п.

У графа на рис.7 δ (v1) = 1; δ (v2) = 2. У графа на рис. 8 степени всех вершин равны нулю.

Рис. 7 Рис. 8

При решении задач и доказательстве теорем использовались разные способы задания графов. На рисунках граф изображался с помощью точек (крутков, квадратиков) и отрезков, соединяющих пары точек. Можно граф представить специальной таблицей. Пользуются еще матричным представлением графа. Выбирают то представление или способ, который удобнее и нагляднее при рассмотрении конкретного вопроса.

Наиболее известный и популярный способ представления графов состоит в геометрическом изображении точек (вершин) и линий (ребер) на бумаге. При численном решении задач на вычислительных машинах граф должен быть представлен дискретным способом. Существует довольно много способов такого рода представления графов. Однако простота использования представления графа, как и эффективность алгоритма, в основе которого он лежит, в полной мере зависит от конкретного выбора этого представления. Одно из направлений теории графов связано с их матричным представлением. Существуют различные виды матриц, ассоциированные с графами. Эти алгебраические формы используются для решения многих задач теории графов. Ниже рассматриваются две такие матричные формы и несколько нестандартных представлений, которые наиболее широко используются в алгоритмах на графах.

Пусть имеем граф G (V, U). Его матрицей смежности называется квадратная матрица (аi, j) порядка n2, где n – число вершин, а аi, j – число ребер, инцидентных вершинам vi и vj. Если граф не имеет кратных ребер, то аi, j = 1, когда vi и vj смежные, и аi, j = 0, когда vi и vj не смежные. Если граф не имеет петель, то все его диагональные элементы равны нулю.

Рассмотрим примеры. На рис. 9 изображены три неориентированных графа. В первом случае (рис.9а) имеем граф без петель и без кратных ребер. Во втором случае (рис.9б) имеем кратные ребра. В третьем случае (рис.9в) в вершинах v1 и v4 имеются петли.

а б в

Рис. 9

Соответствующие этим трем случаям матрицы смежности представлены ниже:

а) 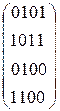б) в)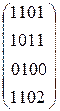

Для неориентированного графа матрица смежности является симметрической. Для ориентированного графа матрица смежности симметрической, вообще говоря, не является.

Матрицей инциденций неориентированного графа, называется матрица (bi,j) размера n · m, где n – число вершин, а m – число ребер, построенная по правилу

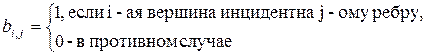
Соответствующие рис.9б матрицы инциденций представлены ниже.

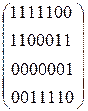
Примечание: для графа на рис. 9б приняты следующие обозначения ребер: Х1 = (v1, v2)1, Х2 = (v1, v2)2, Х3 = (v1, v4)1, Х4 = (v1, v4)2, Х5 = (v1, v4)3, Х6 = (v2, v4), Х7 = (v3, v2).

Матрица инциденций неориентированного графа обладает следующими очевидными свойствами:

1) в графе без петель каждый столбец этой матрицы имеет в точности две единицы, соответствующие паре вершин ребра;

2) если в графе имеются петли, то в столбцах, соответствующих петлям, имеется по одной единице, а в остальных – по две.

Матрицей инциденций ориентированного графа называется матрица (bi, j) размера n · m, где n – число вершин, а m – число ребер, построенная по правилу

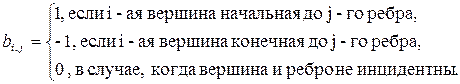
Рассмотрим, например, граф, изображенный на рис.10.

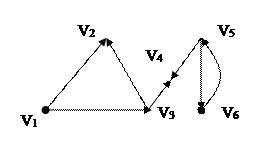
Рис. 10

Построенная в соответствии с описанным правилом матрица инциденций этого графа имеет вид

Примечание: для графа на рис.10 приняты следующие обозначения дуг: Х1 = (v1, v2), Х2 = (v1, v3), Х3 = (v3, v2), Х4 = (v3, v4), Х5 = (v5, v4), Х6 = (v5, v6), Х7 = (v6, v5).

Ориентированный граф, как правило, петель не содержит. Его матрица инциденций имеет в каждом столбце +1 и -1, которые отвечают началу и концу каждого ребра.

Задачи, возникающие на практике, приводят к разного вида операциям над матрицами. Рассмотрим некоторые из них.

Пусть система авиалиний между городами Х1, Х2, Х3 одной страны и городами У1 и У2 другой страны задается подмножеством пар: (Х1, У1), (Х1, У2), (Х2, У1), (Х2, У2), (Х3, У2), т.е. множеством ребер соответствующего графа. Система связи между этими же городами водным транспортом задается другим подмножеством пар: (Х1, У1), (Х2, У1), (Х2, У2), (Х3, У1). Кроме этого, для каждой пары городов (Хi, Уj). Известно число различных водных и авиамаршрутов. Эти числа можно проставить над ребрами на рисунке графа или зафиксировать с помощью двух матриц одинакового порядка:

У1 У2 У1 У2

Х1 4 1 Х1 2 0

А = Х2 2 6 В = Х2 1 3

Х3 0 4 Х3 2 0

Требуется определить, сколькими различными способами с помощью воздушного или водного транспорта можно попасть из каждого города одной страны в каждый город другой страны.

Естественно, что для этого достаточно сложить соответствующие элементы матриц А и В. Ответ можно записать с помощью новой матрицы того же порядка:

У1 У2

Х1 6 1

С = Х2 3 9

Х3 2 4

В общем случае операцию сложения двух матриц можно записать так: если А = (аi,j) и В = (bi,j) – матрицы одного порядка, то матрица С = А + В = (Сi,j), где Сi,j = аi,j + bi,j.

Рассмотрим еще одну задачу. Пусть в каких-то трех странах выделены некоторые города, связанные с транспортом четырех видов: воздушным, железнодорожным, водным и автобусным. Схема транспортных связей между городами Х1 и Х2, принадлежащими первой стране, и городами У1, У2, У3, принадлежащими второй стране, зафиксирована матрицей А, где аi,j показывает на число видов транспорта, соединяющих города Хi и Уi. Аналогичная схема транспортных связей между городами У1, У2, У3, принадлежащими второй стране, и городами Z1, Z2, принадлежащим третьей стране, представлена матрицей В. Какие конкретно виды транспорта связывают пары городов, нас не интересует. Города первой и третьей стран непосредственных связей не имеют.

У1 У2 У3 Z1 Z2

А = Х1 4 0 2 У1 2 1

Х2 2 3 1 В = У2 0 3

У3 3 0

Требуется подсчитать число различных маршрутов от каждого из городов первой страны в каждый из городов третьей страны, проходящих через вторую страну.

Если нарисовать соответствующую схему, то решить задачу не трудно, попробуем решить матричным методом.

Таким образом, по заданным матрицам А и В требуется определить элементы сi,j матрицы С:

Z1 Z2

C = Х1 С11 С12

Х2 С21 С22

Рассуждения определяют матрицу С и алгоритм нахождения элементов сi,j, а именно

Z1 Z2

C = Х1 (а11в11 + а12в21 + а13в31 а11в12 + а12в22 + а13в32

Х2 (а21в11 + а22в21 + а23в31 а21в12 + а22в22 + а23в32

Z1 Z2

C = Х1 14 4

Х2 7 11

Рассмотренная задача убеждает в целесообразности введения еще одной операции над матрицами. Эту операцию принято называть операцией умножения матриц.

Если С = АВ, то элементы матрицы С определяются следующей формулой:

сi,j = ai1в1j + ai2в2j + ai3в3j + … + ainвnj

Таким образом, элемент сi,j образуется из элементов i-й строки матрицы А и элементов j-го столбца матрицы В.

Следует обратить внимание на следующие два факта:

1) операция умножения матрицы А на матрицу В определена только в том случае, если число столбцов в матрице А равно числу строк в матрице В.

2) если матрица А имеет порядок (m x n), а матрица В – порядок (n x r), то матрица – произведение С = АВ имеет порядок (n x m).

Рассмотрим некоторые основные операции, производимые над графами.

Операцией добавления к графу G = <V, U> вершины а образуется граф <V u {a}, U>.

Операцией добавления дуги (а, в) к графу G состоит в образовании графа <V u {a, в), U u {(а, в)}>. При операции удаления дуги, получаем <V, U \ {(а, в)}>. Операции удаления вершины заключается в удалении вершины Vi вместе с инцидентными ей дугами: <V\{Vi}, U \ {(Vj Vk) Vj = Vi или Vk = Vi}>. Операция отождествления вершин (в случае, когда Vi и Vj соединены дугой, операцию называют стягиванием дуги (ViVj).

Пример:

Рис. 11

Из графа G, добавлением вершины 5 образуется граф G1, добавлением дуги (3, 1) – G2, удалением дуги (3, 2) – G3, удалением вершины 2 – G4, отождествлением вершин 1 и 4 – G5, стягиванием дуги (2, 3) – G6.

Добавлением графа без петель G = <V, U> называется граф 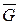= <V, V2 \ (U u i av)>.

Рис. 12

Объединением G1 u G2 называется граф <V1 u V2, U1 u U2>.

Если V1 ∩ V2 ≠ Ø, то пересечением G1 ∩ G2 называется граф <V1 ∩ V2, U1 ∩ U2 >.

Кольцевой суммой G1 + G2, называется граф <V1 u V2, (U1 \ U2) u (U2 \ U2).

Соединением G1 + G2 называется <V1 u V2, U1 u U2 u {[Vi, Vj] | Vi є V2, Vi ≠ Vj}>.

Произведением G1 x G2 называется граф <V1 x V2, U>.

Композицией G1 [G2] называется граф <V1 x V2, U>, в котором ((V1j, V1j), (Vj2, Vj2)) є U, если 1) (Vj1, Vj2) є U1; 2) Vi1 = Vi2, (Vj1, Vj2) є U2.

Рассмотрим специальный класс графов, имеющий важное практическое значение, представители которого именуются деревьями.

Связный неориентированный граф называется деревом, если он не имеет циклов. В частности, дерево не имеет петель и кратных ребер. Граф без циклов есть граф, связные компоненты которого являются деревьями; иногда такой граф называется лесом. Любая цепь в графе без циклов является простой; любая часть такого графа также будет графом без циклов.

Рис. 14 Рис. 15

Пример дерева показан на рис.14, здесь же показаны висячие вершины, на рисунке они выделены закрашенными кружками (вершина дерева, степень которой равна единице, называется висячей вершиной).

Пример леса показан на рис.15.

Постройте какое-нибудь дерево с пятью вершинами и подсчитайте число ребер в полученном графе. Оказывается, что в любом дереве с пятью вершинами всегда будет четыре ребра.

Теорема: дерево с n вершинами имеет n-1 ребро.

Для того, чтобы из одного дерева Г, не являющегося изолированной вершиной, получить два дерева с теми же вершинами, необходимо удалить из Г одно ребро. Для образования трех деревьев необходимо удалить из Г два каких-нибудь ребра. Самое большее из дерева Г с n вершинами можно получить n деревьев, каждое из которых является изолированной вершиной. Для этого необходимо удалить n-1 ребро из дерева Г. Итак, действительно, в дереве с n вершинами n-1 ребро.

Задача. Проводится эксперимент, при котором морскую свинку пускают в лабиринт (рис.16). Сколькими способами она может попасть к пище, если она ни в один тупик не заходит более одного раза, причем, попав в тупик, возвращается на перекресток, с которого свернула в этот тупик. Нарисуйте дерево всевозможных маршрутов морской свинки к пище.

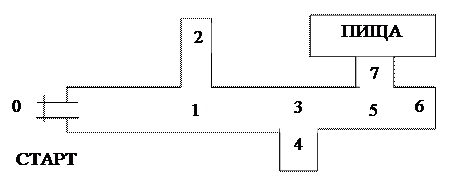
Рис. 16

Ответ: 8 способами

Рис. 17

Дата добавления: 2015-10-13