Теорема 1. Пусть функция f определена и непрерывна со всеми своими производными до порядка n+1

Пусть функция f определена и непрерывна со всеми своими производными до порядка n+ 1 включительно на интервале , где . Пусть далее 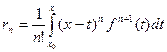(2) (3), где и (4), где . Формула (2) называется остаточным членом формулы Тейлора в интегральной форме.

Формулы (3) и (4) как уже отмечалось ранее в форме Лагранжаи форме Коши соответственно.

► В силу формулы Ньютона – Лейбница . Проинтегрировав по частям интеграл в правой части получим

=

Пусть для некоторого уже доказано, что (5)

Проинтегрировав по частям последний член еще раз

= =

= .

И подставим это выражение в (5) (6)

В результате получилась формула (5) в которой m заменена на m+1, таким образом формула (6) доказана методом индукции для всех , при m=n ее остаточный член имеет вид (2).

Применим теперь обобщенную теорему о среднем к интегралу (2), вынося за знак интеграла среднее значение производной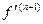

где лежит на интервале с концами и x. Формула (3) доказана.

Если же применить теорему о среднем к интегралу (2) вынося за знак интеграла вреднее значение всей подъинтегральной функции, то получим (7),

где , то есть , где . Отсюда

. Подставив это выражение в (7) получим формулу (4) ◄

Дата добавления: 2015-10-13