Интеграл Стилтьеса.

Пусть на отрезке заданы две функции и 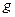. Разобьем на части точками выберем пределы каждого отрезка под точками и составим сумму . Если при сумма стремится к конечному пределу I не зависящему ни от способа дробления, ни от выбора точки , то такая сумма называется интегралом Стилтьеса функции по функции 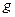и обозначается

Число I есть интеграл Стилтьеса функции по функции 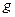если всякому отвечает такое , что при любом способе дробления при котором , будет как бы мы не выбирали точки .

Ясно, что интеграл Римона есть частный случай интеграла Стилтьеса.

1.

2.

3. Если то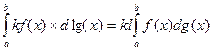

Во всех трех случаях из существования правой части вытекает существование левой части.

4. a<c<b и существуют все три интеграла, входящие в равенство

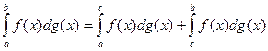, то это равенство справедливо.

Чтобы доказать это свойство интегралов, нужно лишь включить точку c в число точек деления а b при составлении суммы b для интеграла . Нетрудно доказать, что из существования следует существование .

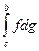Интересно отметить, что обратное предложение неверно.

Пусть f и g заданы на [-1;1], при чем f (x)={

Легко увидеть, что 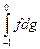существуют (b =0), в то время на не существует. Действительно, раздробим [-1;1] на части так, чтобы 0 не в число точек деления и сост. суммы . Легко понять, что если , то в сумме b останется лишь i слагаемое, ибо если точнее , 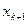лежат по одну сторону.То 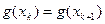,значит b = 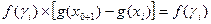В зависимости от того будет 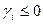ли или будет b =0 или b =1, так, что b не имеет предела.

Свойство и существование одного из интегралов и вытекает из существования другого неравенства , где как обычно положено (1)= 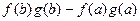(2) Формула (1) называется формулой интегрирования по частям.

►Пусть существует , разделим [a,b] на части и составим сумму .Ее можно представить и так ,откуда . Прибавляя и вычитая правые части выражения (2) находим

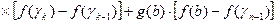. Выражение, стоящее в фигурных скобках, есть ни что иное, как сумма, составленная для интеграла 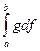, причем точками дробления отрезка[a,b] служат , а точки 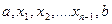суть точки отрезков . Если стремится к 0 max - max , то к 0 стремится и max (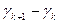) так, что сумма в фигурных скобках стремится к 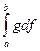,откуда и следует доказ. предлож.

2. Естественно поставить вопрос об условии существования интеграла Стилтьеса. Мы ограничились одной теоремой.

Теорема 1.

существует, если функция f непрерывна на [ a,b ] a g функция ограниченной вариации.

►Достаточно считать, что g(x) возрастает, ибо всякая функция ограниченной вариации есть разность двух возрастающих функций.

Разложим [a,b]. и обозначим соответственно через и 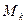наименьшее и наибольшее значение функции на отрезке .

Пусть s , а S .

Ясно, что при любом выборе точек в отрезках окажется

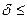s< S

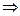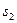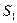Легко проверить, что добавлении поверхностных точек деления сумма s не убывает,а S не возрастает. ни одна сумма s не превосходит сумму S. Действительно имея 2 способа I и II дробления отрезка , которым отвечает суммы и , и мы можем составить способ III, объединяя точки деления I и II. Если способ III отвечает суммам и , то . Так что . Заметив это, обозначим через I верхнюю грань множества {S} всех нижних сумм I=sup{s}. При всяком способе дробления будет в силу неравенства . Если взять произвольное и найти , такое что неравенство влечет неравенство то окажется k=0; n-1 и стало быть .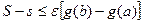

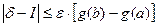Отсюда и подавно при окажется будет иначе говоря lim 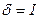так что ◄

Из доказанной теоремы следует, что всякая функция ограниченной вариации интегрируема.

(3).Остановимся на вопросе вычисления интеграла Стилтьеса.

Дата добавления: 2015-10-13