
Читайте также:
|
Теорема 2
Пусть на  задана функция
задана функция  и
и 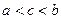 тогда
тогда  , то есть вариация агитивна.
, то есть вариация агитивна.
►Разложим на части каждый из отрезков  и
и  точками
точками  и составим суммы
и составим суммы 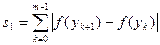
 . Точки
. Точки 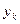 и
и  дробят на части весь отрезок
дробят на части весь отрезок  . Если S сумма отвечающая этому способу дробления, то
. Если S сумма отвечающая этому способу дробления, то  . Отсюда следует, что
. Отсюда следует, что 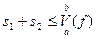 и стало быть неравенство
и стало быть неравенство  (1)
(1)
Теперь разобьем на части  точками
точками  , включив при этом c в число точек деления. Если
, включив при этом c в число точек деления. Если  , то сумма
, то сумма  отвечающая нашему способу деления есть
отвечающая нашему способу деления есть  , где
, где  и
и 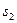 суть суммы, отвечающей отрезку
суть суммы, отвечающей отрезку  и
и  .Отсюда
.Отсюда 
Это неравенство установлено пока лишь для сумм  ,отвечающих таким способом дробления, при которых точка
,отвечающих таким способом дробления, при которых точка  включена в число точек деления. Но так как добавление новых точек деления очевидно не уменьшает сумм
включена в число точек деления. Но так как добавление новых точек деления очевидно не уменьшает сумм  то
то  верно для всех вообще сумм
верно для всех вообще сумм  . Отсюда ясно, что
. Отсюда ясно, что 
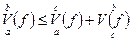

Сопоставляя 
 и
и  , получаем утверждение теоремы.◄
, получаем утверждение теоремы.◄
Следствие 1.
Если в условиях теоремы 
 ,то
,то 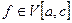 и
и 
 и обратно. Если
и обратно. Если 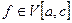 и
и 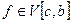 , то
, то  .
.
Дата добавления: 2015-10-13; просмотров: 84 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| При несущественном снижении цены значительно увеличивается спрос | | | Интеграл Стилтьеса. |