Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Задание №3. Найти частные производные от неявных функций

Читайте также:
  1. I. Изменения, позволившие найти выход из тупика
  2. А. Задание.
  3. Абсолютные и производные величины
  4. Армия Спасения открыла первый центр поиска пропавших людей, чтобы помочь семьям найти близких.
  5. В воспитательной работе следует выделить три группы функций.
  6. В то же время, старение тела - это прогрессирую­щий ожог химическими веществами, который приводит к повреждению желез и нарушению их функций, вплоть до их полой дисфункции.
  7. ВИД ФУНКЦИЙ ПОЛЕЗНОСТИ И РИСКОВАННЫЕ РЕШЕНИЯ

Вариант № 1.

Вариант № 2.

Вариант № 3.

Вариант № 4.

Вариант № 5.

Вариант № 6.

Вариант № 7.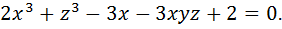

Вариант № 8.

Вариант № 9.

Вариант № 10.

Вариант № 11.

Вариант № 12.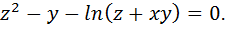

Вариант № 13.

Вариант № 14.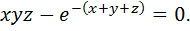

Вариант № 15.

Вариант № 16.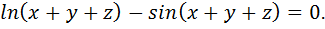

Вариант № 17.

Вариант № 18.

Вариант № 19.

Вариант № 20.

Вариант № 21.

Вариант № 22.

Вариант № 23.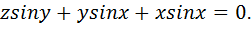

Вариант № 24.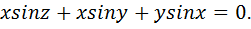

Вариант № 25. .

Вариант № 26. .

Вариант № 27. .

Вариант № 28. .

Вариант № 29.

Вариант № 30.

Задание №4. Написать уравнение касательной плоскости и нормали в точке М к поверхности, заданной уравнением

или .

Вариант № 1. .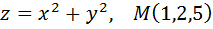

Вариант № 2. .

Вариант № 3. .

Вариант № 4. .

Вариант № 5. .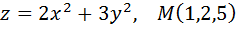

Вариант № 6. .

Вариант № 7. .

Вариант № 8. .

Вариант № 9. .

Вариант № 10. .

Вариант № 11. .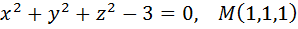

Вариант № 12. .

Вариант № 13. .

Вариант № 14. .

Вариант № 15. .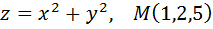

Вариант № 16. .

Вариант № 17. .

Вариант № 18. .

Вариант № 19. .

Вариант № 20. .

Вариант № 21. .

Вариант № 22. .

Вариант № 23. .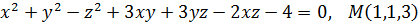

Вариант № 24. .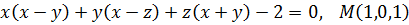

Вариант № 25. .

Вариант № 26. .

Вариант № 27. .

Вариант № 28. .

Вариант № 29. .

Вариант № 30. .

Дата добавления: 2015-10-13; просмотров: 103 | Нарушение авторских прав

Читайте в этой же книге: Задание №1. Решить задачи, используя скалярное произведение векторов. | Задание №2. Доказать, что векторы образуют базис и написать разложение вектора по векторам этого базиса. | Задание №4. Вычислить объем тетраэдра с вершинами в точках A, B, C, D и высоту, опущенную из вершины D на грань ABC. | Медианы, проведенной из вершины С. | Задание №5. Преобразовать уравнение кривой в полярной системе координат и построить кривую. | Задание №3. Решить систему уравнений с помощью обратной матрицы | Задание №3. Вычислить пределы, не пользуясь правилом Лопиталя | Задание №1. Найти производные функций | Правила Лопиталя | Задание № 5. Найти наибольшее и наименьшее значение функции на заданном отрезке. |
<== предыдущая страница | следующая страница ==>
Задание №1. Найти область определения функции. Ответ проиллюстрировать графически.| Задание №5. Исследовать заданную функцию на экстремум
mybiblioteka.su - 2015-2024 год. (0.009 сек.)