
Читайте также:
|
Вариант№1. 
Вариант№2. 
Вариант№3. 
Вариант№4. 
Вариант№5. 
Вариант№6. 
Вариант№7. 
Вариант№8. 
Вариант№9. 
Вариант№10. 
Вариант№11. 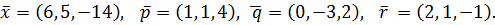
Вариант№12. 
Вариант№13. 
Вариант№14. 
Вариант№15. 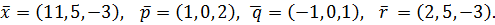
Вариант№16. 
Вариант№17. 
Вариант№18. 
Вариант№19. 
Вариант№20. 
Вариант№21. 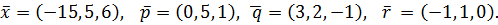
Вариант№22. 
Вариант№23. 
Вариант№24. 
Вариант№25. 
Вариант№26. 
Вариант№27. 
Вариант№28. 
Вариант№29. 
Вариант№30. 
Задание №3. Даны векторы, выраженные через векторы. Известны модули векторов и угол между ними. Вычислить площадь параллелограмма, построенного на векторах.
Вариант№1. 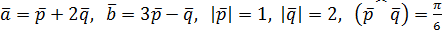 .
.
Вариант№2. 
Вариант№3. 
Вариант№4. 
Вариант№5. 
Вариант№6. 
Вариант№7. 
Вариант№8.  .
.
Вариант№9. 
Вариант№10. 
Вариант№11.  .
.
Вариант№12.  .
.
Вариант№13. 
Вариант№14. 
Вариант№15. 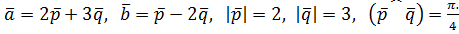
Вариант№16. 
Вариант№17.  .
.
Вариант№18. 
Вариант№19. 
Вариант№20. 
Вариант№21. 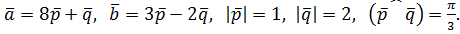
Вариант№22. 
Вариант№23.  .
.
Вариант№24.  .
.
Вариант№25. 
Вариант№26.  .
.
Вариант№27.  .
.
Вариант№28. 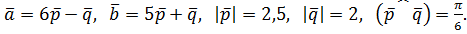
Вариант№29.  .
.
Вариант№30.  .
.
Дата добавления: 2015-10-13; просмотров: 92 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание №1. Решить задачи, используя скалярное произведение векторов. | | | Задание №4. Вычислить объем тетраэдра с вершинами в точках A, B, C, D и высоту, опущенную из вершины D на грань ABC. |