Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Задание №3. Вычислить пределы, не пользуясь правилом Лопиталя

Читайте также:
  1. V. Вычислить двойной интеграл, перейдя к полярным координатам.
  2. VI. Вычислить криволинейный интеграл.
  3. А. Задание.
  4. Б) Вычислить несобственный интеграл или установить его расходимость.
  5. БОЛЬШОЙ ГРЕХ ДЕЛАЕТ ЧЕЛОВЕК, ЕСЛИ, ПОЛЬЗУЯСЬ ТРУДАМИ ЛЮДЕЙ, САМ НЕ РАБОТАЕТ
  6. Выберите один правильный ответ на тест-задание
  7. Вычислить поток векторного поля через поверхность W.

Вариант№ 1.

.

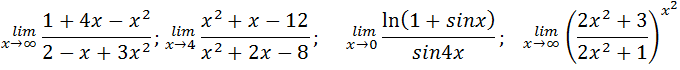
Вариант№ 2.

Вариант№ 3.

Вариант№ 4.

Вариант№ 5.

Вариант№ 6.

Вариант№ 7.

Вариант№ 8.

Вариант№ 9.

Вариант№ 10.

Вариант№ 11.

Вариант№ 12.

Вариант№ 13.

 

Вариант№ 14.

 

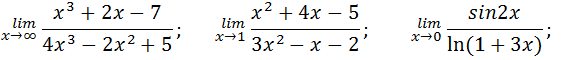
Вариант№ 15.

Вариант№ 16.

Вариант№ 17.

Вариант№ 18.

 

 

Вариант№ 19.

Вариант№ 20.

Вариант№ 21.

Вариант№ 22.

Вариант№ 23.

Вариант№ 24.

Вариант№ 25.

Вариант№ 26.

Вариант№ 27.

Вариант№ 28.

Вариант№ 29.

Вариант№ 30.

Задание №4. Найти точки разрыва функции и построить график

Вариант№ 1.

Вариант№ 2.

Вариант№ 3.

Вариант№ 4.

Вариант№ 5.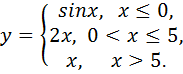

Вариант№ 6.

Вариант№ 7.

Вариант№ 8.

Вариант№ 9.

Вариант№ 10.

Вариант№ 11.

Вариант№ 12.

Вариант№ 13.

Вариант№ 14.

Вариант№ 15.

Вариант№ 16.

Вариант№ 17.

Вариант№ 18.

Вариант№ 19.

Вариант№ 20.

Вариант№ 21.

Вариант№ 22.

Вариант№ 23.

Вариант№ 24.

Вариант№ 25.

Вариант№ 26.

Вариант№ 27.

Вариант№ 28.

Вариант№ 29.

Вариант№ 30.

 

Тема 5. Производная и ее приложения

Теоретические вопросы

 

1. Определение производной функции в точке.

2. Механический смысл производной.

3. Геометрический смысл производной.

4. Уравнение касательной и нормали в заданной точке.

5. Таблица производных.

6. Правила дифференцирования.

7. Дифференцирование сложной функции.

8. Дифференцирование обратной функции.

9. Дифференцирование функции заданной параметрически.

10. Дифференцирование функции заданной неявно.

11. Дифференцируемость функции в точке. Дифференциал (определение, геометрический смысл).

12. Приближенные вычисления с помощью дифференциала.

13. Производные и дифференциалы высших порядков.

14. Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа, Коши).

15. Исследование функции на монотонность (необходимые и достаточные условия).

16. Экстремумы. Необходимое и достаточное условия экстремума.

17. Выпуклость, вогнутость, точки перегиба графика функции.

18. Асимптоты графика функции.

19. Общая схема исследования функции.

20. Векторная функция скалярного аргумента.

Варианты заданий

Дата добавления: 2015-10-13; просмотров: 213 | Нарушение авторских прав

Читайте в этой же книге: Задание №1. Решить задачи, используя скалярное произведение векторов. | Задание №2. Доказать, что векторы образуют базис и написать разложение вектора по векторам этого базиса. | Задание №4. Вычислить объем тетраэдра с вершинами в точках A, B, C, D и высоту, опущенную из вершины D на грань ABC. | Медианы, проведенной из вершины С. | Задание №5. Преобразовать уравнение кривой в полярной системе координат и построить кривую. | Правила Лопиталя | Задание № 5. Найти наибольшее и наименьшее значение функции на заданном отрезке. | Задание №1. Найти область определения функции. Ответ проиллюстрировать графически. | Задание №3. Найти частные производные от неявных функций | Задание №5. Исследовать заданную функцию на экстремум |
<== предыдущая страница | следующая страница ==>
Задание №3. Решить систему уравнений с помощью обратной матрицы| Задание №1. Найти производные функций
mybiblioteka.su - 2015-2024 год. (0.017 сек.)