Читайте также:
|
1. 
; W— внешняя часть поверхности, образованная цилиндром 
и плоскостями z=0, z=3
2. 
; W— внешняя часть поверхности, образованная полусферой 
и плоскостью z=0
3. 
; W— верхняя сторона треугольника, вырезанная из плоскости x+y+z=1 координатными плоскостями
4. 
; W— внешняя часть поверхности, образованная сферой 
и параболоидом 
5. 
; W— внешняя часть поверхности, образованная конусом 
и параболоидом 
6. 
; W— внешняя часть поверхности, образованная параболоидом 
и плоскостью z=0
7. 
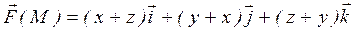; W— внешняя часть поверхности, образованная цилиндром 
и плоскостями z=х, z=0
8. 
; W— внешняя часть поверхности, образованная цилиндром 
и плоскостями z=0, z=3
9. 
; W— полная поверхность пирамиды, ограниченной плоскостями x=0, y=0, z=0, x+y+z=a, a>0
10. 
; W— внешняя часть поверхности, образованная конусом 
и параболоидом 
11. 
; W— внешняя часть поверхности, образованная цилиндром 
и плоскостями z=y, z=0
12. 
; W— верхняя часть плоскости 2x+y+z=3, лежащая в первом октанте
13. 
; W— внешняя часть поверхности, образованная цилиндром 
, плоскостью y=0 и параболоидом 
14. 
; W— верхняя часть плоскости x-2y+z=2, лежащая в первом октанте
15. 
; W— внешняя часть поверхности, образованная поверхностями 
, z=0, 
16. 
; W— верхняя часть плоскости x-3y+2z-2=0, лежащая в первом октанте
17. 
; W— внешняя часть замкнутой поверхности, лежащая в первом октанте и ограниченная поверхностями 
, z=0, x=0, y=0
18. 
; W— верхняя часть плоскости x-2y+2z-2=0, лежащая в первом октанте
19. 
; W— верхняя часть плоскости –x+2y+2z-2=0, лежащая в первом октанте
20. 
; W— внешняя часть поверхности, образованная параболоидом 
и плоскостями y=1, z=0, x=0
21. 
; W— верхняя часть плоскости 2x+y+z-2=0, лежащая в первом октанте
22. 
; W— внешняя часть поверхности, образованная конусом 
и плоскостью z=0
23. 
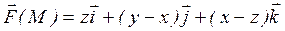; W— верхняя часть плоскости x-y+z-2=0, лежащая в первом октанте
24. 
; W— внешняя часть поверхности, образованная параболоидом 
и плоскостью z=0
25. 
; W— внешняя часть поверхности, образованная цилиндром 
и плоскостями x=0, y=0, z=0, z=4
26. 
, W— внешняя часть поверхности; образованная, параболоидом 
и плоскостью z=0
27. 
; W— верхняя сторона треугольника, вырезанная из плоскости 3x-2y+2z=6 координатными плоскостями
28. 
; W— внешняя часть поверхности, образованная, сферой 
и плоскостью z=0
29. 
; W— верхняя сторона треугольника, вырезанная из плоскости -2x+y+z=4 координатными плоскостями.
30. 
; W— внешняя часть поверхности, образованная цилиндром 
, плоскостью z=0 и параболоидом 
.
4**. Вычислить циркуляцию вектора 
по контуру L:
1. 
, L — линия пересечения поверхностей 
, 
, z>0
2. 
, L — линия пересечения поверхностей 
, 
3. 
, L — периметр треугольника с вершинами А(а;0;0), В(0;а;0), С(0;0;а)
4. 
, L — линия пересечения поверхностей x=0, y=0, z=0, 
5. 
, L — линия пересечения поверхностей 
, x=0, y=0, z=2
6. 
, L — линия пересечения поверхностей 
, z=1
7. 
, L — линия пересечения поверхностей z=0, 
8. 
, L — линия пересечения поверхностей x=0, y=0, z=0, 
9. 
, L — линия пересечения поверхностей x=0, y=0, z=0, 
10. 
, L — линия пересечения поверхностей x=0, y=0, z=0,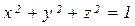 
11. 
, L — периметр треугольника с вершинами А(1;0;0), В(0;1;0), С(0;0;1)
12. 
, L — линия пересечения поверхностей 
, y=4
13. 
, L — линия пересечения поверхностей x=0, y=0, z=0, 
14. 
, L — линия пересечения поверхностей 
, x=0, y=0, z=0
15. 
, L — линия пересечения поверхностей 
, x=0, y=0, z=0
16. 
, L — линия пересечения поверхностей 
, x=0, y=0, z=0
17. 
, L — периметр треугольника с вершинами А(a;0;0), В(0;a;0), С(0;0;a)
18. 
, L — периметр треугольника с вершинами А(0;-1), В(0;2), С(2;0)
19. 
, L — периметр треугольника с вершинами А(1;0;0), В(0;1;0), С(0;0;1)
20. 
, L — линия пересечения поверхностей 
, z=0
21. 
, L — линия пересечения поверхностей z= -1, 
22. 
, L — линия пересечения поверхностей 
, x=0, y=0, z=0
23. 
, L — линия пересечения поверхностей 
, x=0, y=0, z=0
24. 
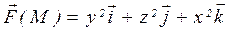, L — линия пересечения поверхностей 
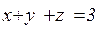, x=0, y=0, z=0
25. 
, L — линия пересечения поверхностей 
, x=0, y=0, z=0
26. 
, L — линия пересечения поверхностей , x=0, y=0, z=0
27. 
, L — периметр треугольника с вершинами А(2;0;0), В(0;2;0), С(0;0;2)
28. 
, L — линия пересечения поверхностей x=0, y=0, z=0, 
29. 
, L — линия пересечения поверхностей x=0, y=0, z=2, 
30. 
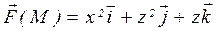, L — линия пересечения поверхностей z=4, 
Дата добавления: 2015-10-13; просмотров: 177 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Найти работу силы при перемещении материальной точки | | | Проверить, будет ли потенциальным и соленоидальным поле . |