
Читайте также:
|
Контрольная работа 11
Криволинейные и поверхностные интегралы
Найти работу силы при перемещении материальной точки
вдоль линии L от точки M к точке N:
1. 
2. 
3. 
4. 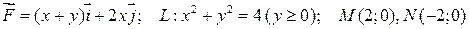
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 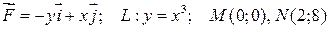
30. 
2*. Вычислить интеграл по замкнутому контуру, применив формулу Грина:
1.  , где L — треугольник с вершинами А(а;0), В(а;а), С(0;а)
, где L — треугольник с вершинами А(а;0), В(а;а), С(0;а)
2. 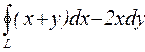 , где L —контур треугольника со сторонами x=0, y=0, x+y=a
, где L —контур треугольника со сторонами x=0, y=0, x+y=a
3.  , где L —контур треугольника с вершинами А(1;1), В(2;1), С(2;2)
, где L —контур треугольника с вершинами А(1;1), В(2;1), С(2;2)
4.  , где L — окружность
, где L — окружность 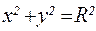
5.  , где L —контур, образованный полуокружностью
, где L —контур, образованный полуокружностью
 и осью ОХ
и осью ОХ
6.  , где L —контур, образованный линиями y=sinx и y=0,
, где L —контур, образованный линиями y=sinx и y=0, 
7.  , где L —окружность
, где L —окружность 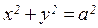
8.  , где L — треугольник с вершинами О(0;0), А(1;0), В(0;1)
, где L — треугольник с вершинами О(0;0), А(1;0), В(0;1)
9.  , где L — треугольник с вершинами А(1;1), В(2;2), С(1;3)
, где L — треугольник с вершинами А(1;1), В(2;2), С(1;3)
10.  , где L — окружность
, где L — окружность 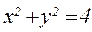
11.  , где L — контур, образованный параболой
, где L — контур, образованный параболой  и ее хордой АВ; А(1;0), В(2;3)
и ее хордой АВ; А(1;0), В(2;3)
12.  , где L — окружность
, где L — окружность 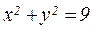
13.  , где L — контур прямоугольника
, где L — контур прямоугольника 
14.  , где L — треугольник с вершинами А(2;0), О(0;0), и В(4;2)
, где L — треугольник с вершинами А(2;0), О(0;0), и В(4;2)
15.  , где L — контур, образованный линиями
, где L — контур, образованный линиями 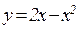 и y=0
и y=0
16.  , где L — контур треугольника с вершинами А(2;0), О(0;0), и В(0;2)
, где L — контур треугольника с вершинами А(2;0), О(0;0), и В(0;2)
17.  , где L — треугольник с вершинами А(0;0), В(3;0), и С(0;3)
, где L — треугольник с вершинами А(0;0), В(3;0), и С(0;3)
18.  , где L — окружность
, где L — окружность 
19. 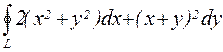 , где L — окружность
, где L — окружность 
20.  , где L — треугольник с вершинами А(0;0), В(0;2), С(4;0)
, где L — треугольник с вершинами А(0;0), В(0;2), С(4;0)
21.  , где L —треугольник с вершинами А(5;0), В(5;5), С(0;5)
, где L —треугольник с вершинами А(5;0), В(5;5), С(0;5)
22.  , где L —контур треугольника со сторонами x=1, y=1, x+y=3
, где L —контур треугольника со сторонами x=1, y=1, x+y=3
23. 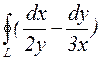 , где L —контур треугольника с вершинами А(1;1), В(2;1), С(2;2)
, где L —контур треугольника с вершинами А(1;1), В(2;1), С(2;2)
24.  , где L — контур, образованный полуокружностью
, где L — контур, образованный полуокружностью  и осью ОХ
и осью ОХ
25.  , где L — контур, образованный линиями y=2sinx и y=0,
, где L — контур, образованный линиями y=2sinx и y=0, 
26.  , где L — окружность
, где L — окружность 
27. 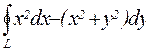 , где L — треугольник с вершинами О(0;0), А(2;0), и В(0;4)
, где L — треугольник с вершинами О(0;0), А(2;0), и В(0;4)
28. 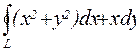 , где L — треугольник с вершинами А(1;1), В(1;5), и С(5;5)
, где L — треугольник с вершинами А(1;1), В(1;5), и С(5;5)
29.  , где L — окружность
, где L — окружность 
30.  , где L — контур, образованный параболой
, где L — контур, образованный параболой  и ее хордой АВ; А(2;0), В(-1;-3)
и ее хордой АВ; А(2;0), В(-1;-3)
Дата добавления: 2015-10-13; просмотров: 312 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ток-шоу | | | Вычислить поток векторного поля через поверхность W. |