Проверить, будет ли потенциальным и соленоидальным поле .

В случае потенциальности поля найти его потенциал :

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

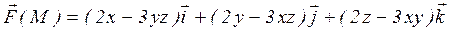
20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

6*. Выполнить задание, применив криволинейный интеграл первого рода:

1. Вычислить длину дуги кривой , если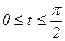

2. Вычислить длину полукубической параболы от точки О(0;0) до точки А(5; )

3. Найти массу четверти дуги эллипса , если плотность в каждой точке линии равна произведению координат этой точки

4. Вычислить , где L – отрезок прямой ОВ; О(1;2) и В(2;4)

5. Вычислить длину дуги линии от t=0 до t=

6. Найти массу первой четверти витка винтовой линии если плотность в каждой точке пропорциональна её абсциссе

7. Найти длину дуги полуарки циклоиды

8. Найти длину дуги конической винтовой линии если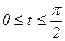

9. Найти момент инерции относительно оси OZ первого витка линии

10. Найти статический момент первого витка винтовой линии

относительно плоскости YOX

11. Вычислить криволинейный интеграл , где L – дуга развертки окружности

12.Вычислить интеграл , где L – дуга кривой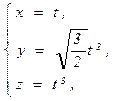

13. Найти статический момент дуги эллипса относительно оси OX, если плотность в каждой точке линии равна ее абсциссе

14. Вычислить криволинейный интеграл вдоль линии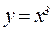

15. Найти массу дуги кривой , если линейная плотность в каждой точке равна

16. Вычислить площадь, ограниченную эллипсом

17.Найти массу дуги линии 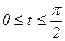, если линейная плотность ее пропорциональна ординате точки

18.Найти момент инерции линии 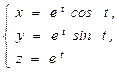относительно оси OZ, если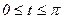

19. Найти статический момент винтовой линии относительно плоскости XOZ, если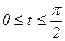

20. Вычислить криволинейный интеграл , если АВ – дуга полукубической параболы от точки А(3; ) до точки В(8; )

21. Вычислить , где L – полуокружность

22. Найти массу четверти окружности , расположенной в первом октанте, если плотность в каждой точке пропорциональна абсциссе этой точки

23.Найти массу дуги астроиды 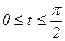, если плотность

24. Найти массу четверти окружности , расположенной в первом октанте, если ее плотность в каждой точке пропорциональна значению ординаты этой точки в третьей степени

25. Вычислить криволинейный интеграл вдоль линии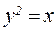

26. Найти массу дуги кривой , если линейная плотность в каждой точке пропорциональна значению ординаты

27. Найти статический момент линии относительно плоскости ХOZ, если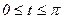

28. Найти длину дуги конической винтовой линии если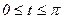

29. Найти момент инерции относительно оси OХ первого витка линии

30. Найти статический момент первого витка винтовой линии относительно оси OX

7*. Выполнить задание, применив поверхностный интеграл первого рода:

1.Вычислить , где s:

2.Вычислить , s: ; z=0.

3. Найти массу поверхности куба , если плотность

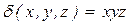
4. Найти момент инерции части боковой поверхности конуса , 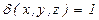относительно оси OZ

5.Вычислить 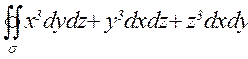, где s - сфера

6.Вычислить 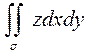, s:

7. Найти массу сферы, если поверхностная плотность в каждой точке равна квадрату расстояния от этой точки до некоторого фиксированного диаметра сферы

8. Вычислить , s: ; z= 1.

9. Вычислить 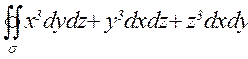, s: .

10. Вычислить , где s - положительная сторона нижней половины сферы

11. Найти момент инерции поверхности параболоида , ограниченного плоскостью z=2, относительно оси OX

12. Применив формулу Стокса, вычислить , где С- кривая

13. Вычислить поверхностный интеграл ,

где s - внешняя сторона пирамиды, образованной плоскостями x=0, y=0, z=0, x+y+z=1

14.Определить статический момент относительно плоскости OXY однородной полусферы ,

15. Вычислить , где s - внешняя поверхность конуса

16. Вычислить , где s - наружная сторона пирамиды, образованной плоскостями x=0, y=0, z=0, x+y+z=а

17. Вычислить 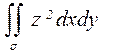, где s - внешняя сторона эллипсоида

18. Вычислить , где s - внешняя сторона

поверхности

19. Применив формулу Стокса, вычислить , где С- кривая

20. Применив формулу Стокса, вычислить , где С- окружность , z=0

21.Найти массу сферы, если поверхностная плотность в каждой точке равна расстоянию от этой точки до некоторого фиксированного диаметра сферы

22.Вычислить , если s ограничена поверх-ностями , z=-4, z=4

23. Вычислить , где s - положительная сторона куба, составленного плоскостями x=0, y=0, z=0, x=1, y=1, z=1

24. Вычислить 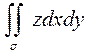, где s - внешняя сторона эллипсоида

25. Вычислить 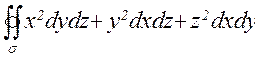, где s - внешняя сторона поверхности куба

26. Найти момент инерции поверхности параболоида , ограниченного плоскостью z=5 относительно оси OY

27. Вычислить поверхностный интеграл , где s - внешняя сторона пирамиды, образованной плоскостями x=0, y=0, z=0, x+y+z=3

28.Определить статический момент относительно плоскости OXZ однородной полусферы ,

Дата добавления: 2015-10-13