
Введение
В третьем семестре студенты должны выполнить 3 контрольные работы по темам: «Кратные интегралы», «Криволинейные и поверхностные интегралы», «Ряды».
Порядковый номер задания соответствует выбранному варианту, номер которого определяет преподаватель. Количество и порядок решения заданий могут меняться по его усмотрению. Необходимые знания, понятия, правила излагаются на практических занятиях по курсу.
Задания, отмеченные одной звездочкой, требуют точного выполнения чертежа на миллиметровой бумаге или применения знаний по начертательной геометрии. Задания, отмеченные двумя звездочками, являются заданиями повышенной сложности и требуют объемных вычислений. И, наконец, задание, отмеченное тремя звездочками, требует применения компьютера.
По просьбе преподавателя задания, отмеченные звездочками, могут быть оформлены в виде рефератов или научных работ студентов.
Контрольная работа 10
Кратные интегралы
1*.Изменить порядок интегрирования:
1. а)  ; б)
; б) 
2. а)  ; б)
; б) 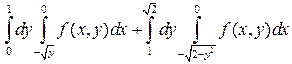
3. а)  ; б)
; б) 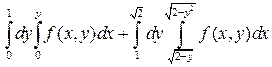
4. а)  ; б)
; б) 
5. а)  ; б)
; б) 
6. а)  ; б)
; б) 
7. а)  ; б)
; б) 
8. а)  ; б)
; б) 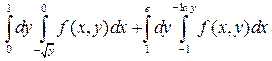
9. а) 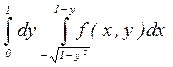 ; б)
; б) 
10. а)  ; б)
; б) 
11. а) 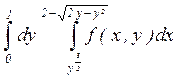 ; б)
; б) 
12. а)  ; б)
; б) 
13. а)  ; б)
; б) 
14. а) 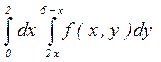 ; б)
; б) 
15. а)  ; б)
; б) 
16. а)  ; б)
; б) 
17. а) 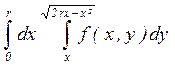 ; б)
; б) 
18. а)  ; б)
; б) 
19. а)  ; б)
; б) 
20. а)  ; б)
; б) 
21. а) 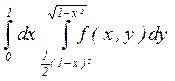 ; б)
; б) 
22. а)  ; б)
; б) 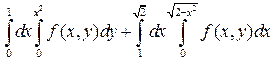
23. а)  ; б)
; б) 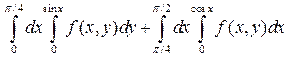
24. а)  ; б)
; б) 
25. а) 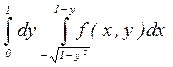 ; б)
; б) 
26. а)  ; б)
; б) 
27. а)  ; б)
; б) 
28. а)  ; б)
; б) 
29. а)  ; б)
; б) 
30. а)  ; б)
; б) 
2*.Вычислить двойные интегралы:
1.а)  , где D: x=0, y=0,
, где D: x=0, y=0,  ;
;
б)  , где D: меньшая часть круга
, где D: меньшая часть круга  , отсекаемая
, отсекаемая
прямой y=x
2.а)  , где D: y=4, y=x2,
, где D: y=4, y=x2,  (x>0);
(x>0);
б)  , где D:
, где D: 
3.а)  , где D: x=2, y=x,
, где D: x=2, y=x,  ;
;
б)  , где D:
, где D: 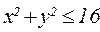
4.а) 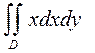 , где D: y-x=2, y=x2;
, где D: y-x=2, y=x2;
б)  , где D: верхняя часть области, ограниченная линией
, где D: верхняя часть области, ограниченная линией 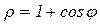 и полярной осью
и полярной осью
5.а)  , где D:
, где D:  , y=x, y=2-x2;
, y=x, y=2-x2;
б)  , где D:
, где D: 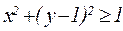 ,
,  , (y>0, x>0)
, (y>0, x>0)
6.а) 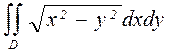 , где D: треугольник с вершинами О(0;0),
, где D: треугольник с вершинами О(0;0),
А(1;-1), В(1;1);
б)  , где D:
, где D: 
7.а) 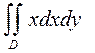 , где D: y=1+x2, y=5;
, где D: y=1+x2, y=5;
б)  , где D:
, где D:  , y=x,
, y=x, 
8.а)  , где D: x=y2, y=x2;
, где D: x=y2, y=x2;
б)  , где D:
, где D: 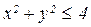
9.а)  , где D: x=0, y=0, x=1,
, где D: x=0, y=0, x=1,  ;
;
б)  , где D:
, где D: 
10.а) 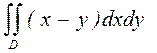 , где D: x=1, x=3, y=x, y=x2;
, где D: x=1, x=3, y=x, y=x2;
б) 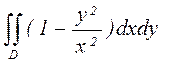 , где D:
, где D: 
11.а)  , где D: треугольник с вершинами О(0;0), А(1;1), В(0;1);
, где D: треугольник с вершинами О(0;0), А(1;1), В(0;1);
б)  , где D:
, где D: 
12.а)  , где D: треугольник с вершинами О(0;0), А(1;-1), В(1;1);
, где D: треугольник с вершинами О(0;0), А(1;-1), В(1;1);
б)  , где D:
, где D: 
13.а)  , где D: y2=x, x=0, y=1;
, где D: y2=x, x=0, y=1;
б)  , где D: полукруг диаметром
, где D: полукруг диаметром  с центром в точке
с центром в точке 
14.а)  , где D: треугольник с вершинами О(0;0), А(10;1), В(1;1);
, где D: треугольник с вершинами О(0;0), А(10;1), В(1;1);
б) 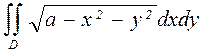 , где D:
, где D: 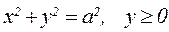
15.а)  , где D: x2+(y-1)2=1, x+y=2,
, где D: x2+(y-1)2=1, x+y=2,  ;
;
б) 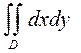 , где D:
, где D:  (область, не содержащая полюса)
(область, не содержащая полюса)
16.а)  , где D: x=1, x=2, y=x, y=x2;
, где D: x=1, x=2, y=x, y=x2;
б) 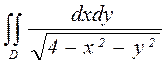 , где D:
, где D: 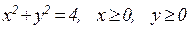
17.а)  , где D:
, где D:  ;
;
б)  , где D:
, где D: 
18.а)  , где D: x=0, x=p, y=0, y=1+cosx;
, где D: x=0, x=p, y=0, y=1+cosx;
б) 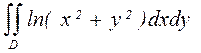 , где D:
, где D: 
19.а)  , где D: y=
, где D: y= 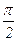 , y=-
, y=- 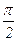 , x=0, x=3cosy;
, x=0, x=3cosy;
б)  , где D:
, где D: 
20.а) 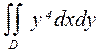 , где D: x=0, x=
, где D: x=0, x= 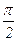 , y=1, y=cosx;
, y=1, y=cosx;
б)  , где D:
, где D: 
21.а)  , где D: y2 =2x, x=1;
, где D: y2 =2x, x=1;
б)  , где D:
, где D: 
22.а)  , где D: y=2-x2, y=2x-1;
, где D: y=2-x2, y=2x-1;
б)  , где D:
, где D: 
23.а)  , где D: x=0, x=2p, y=0, y=a;
, где D: x=0, x=2p, y=0, y=a;
б)  , где D:
, где D:  .
.
24.а)  , где D: x=0, x=1, y=x, y=2x;
, где D: x=0, x=1, y=x, y=2x;
б)  , где D: x=0, x=1, y=0,
, где D: x=0, x=1, y=0, 
25.а)  , где D: x=1, x=3, y=x, y=x3;
, где D: x=1, x=3, y=x, y=x3;
б)  , где D:
, где D: 
26.а)  , где D: xy=1, y=
, где D: xy=1, y= 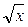 , x=2;
, x=2;
б)  , где D:
, где D: 
27.а)  , где D: x=0, y=0, 4x+4y-p=0;
, где D: x=0, y=0, 4x+4y-p=0;
б)  , где D:
, где D: 
28.а)  , где D: y=x2, y2 =x;
, где D: y=x2, y2 =x;
б)  , где D:
, где D: 
29.а)  , где D: x=2, y=x, xy=1;
, где D: x=2, y=x, xy=1;
б)  , где D:
, где D: 
30.а)  , где D: y=1, y=2, x=0, x=lny;
, где D: y=1, y=2, x=0, x=lny;
б) 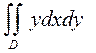 , где D: полукруг диаметром 2 с центром в точке С(1;0).
, где D: полукруг диаметром 2 с центром в точке С(1;0).
3*. Вычислить тройные интегралы:
1.а)  , где V: x=0, y=0, z=0, x+y=1, x2+z2=1;
, где V: x=0, y=0, z=0, x+y=1, x2+z2=1;
б)  , где V: z=x2+y2, z=4
, где V: z=x2+y2, z=4
2.а)  , где V: x2 +y2+z2=1,
, где V: x2 +y2+z2=1,  ;
;
б)  , где V: x2+z2=1, y=0, y=1
, где V: x2+z2=1, y=0, y=1
3.а)  , где V: x=1, x=3, y=0, y=2, z=2, z=5;
, где V: x=1, x=3, y=0, y=2, z=2, z=5;
б)  , где V: 3z=x2+y2, z=3
, где V: 3z=x2+y2, z=3
4.а)  , где V: x=0, y=0, z=0, x+y+z=1;
, где V: x=0, y=0, z=0, x+y+z=1;
б)  , где V: 2z=x2+y2, z=2
, где V: 2z=x2+y2, z=2
5.а)  , где V: x=0, y=1, z=0, y=3, x+2z=3;
, где V: x=0, y=1, z=0, y=3, x+2z=3;
б) 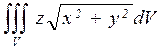 , где V: x2+y2-2x=0, z=0, z=5
, где V: x2+y2-2x=0, z=0, z=5
6.а) 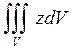 , где V:
, где V:  , y=x, y=2x;
, y=x, y=2x;
б) 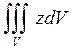 , где V: x2+y2-z2 =0, z=2
, где V: x2+y2-z2 =0, z=2
7.а)  , где V:
, где V:  ;
;
б)  , где V: x2+y2-z2 =0, z=6-x2-y2, z>0
, где V: x2+y2-z2 =0, z=6-x2-y2, z>0
8.а)  , где V: x=0, y=0, z=0, x=1, y=1, x+y+z=2;
, где V: x=0, y=0, z=0, x=1, y=1, x+y+z=2;
б) 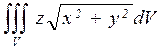 , где V: x2+y2=2x, y=0, z=0, z=a, (a>0)
, где V: x2+y2=2x, y=0, z=0, z=a, (a>0)
9.а)  , где V: x=0, y=0, z=0, x=2, y=2, x+y+z=4;
, где V: x=0, y=0, z=0, x=2, y=2, x+y+z=4;
б) 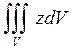 , где V: z=6-x2-y2, x2+y2=z2, z>0
, где V: z=6-x2-y2, x2+y2=z2, z>0
10.а)  , где V: x=0, y=0, x=1, y=1, z=0, x+y+z=2;
, где V: x=0, y=0, x=1, y=1, z=0, x+y+z=2;
б)  , где V: z=x2+y2, z=4
, где V: z=x2+y2, z=4
11.а)  , где V: x=0, z=0, y=1, y=3, x+2z=3;
, где V: x=0, z=0, y=1, y=3, x+2z=3;
б) 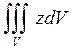 , где V: z2 =x2+y2, z=1
, где V: z2 =x2+y2, z=1
12.а)  , где V: x=0, y=0, z=0, y=1, x+z=1;
, где V: x=0, y=0, z=0, y=1, x+z=1;
б) 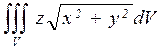 , где V: x2+y2=1, z=0, z=5
, где V: x2+y2=1, z=0, z=5
13.а)  , где V: x=0, y=0, z=0, y=2, x+z=3;
, где V: x=0, y=0, z=0, y=2, x+z=3;
б)  , где V:
, где V: 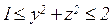 ,
, 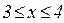
14.а)  , где V: x=1, x=3, y=0, y=2, z=2, z=5;
, где V: x=1, x=3, y=0, y=2, z=2, z=5;
б)  , где V: x2+y2=1, 2x+3z=6, z=0
, где V: x2+y2=1, 2x+3z=6, z=0
15.а)  , где V: x=±1, y=±1, z=0,
, где V: x=±1, y=±1, z=0,  ;
;
б)  , где V:
, где V:  ,
,  ,
, 
16.а)  , где V: x=0, y=0, z=3, z=6, x+y=1;
, где V: x=0, y=0, z=3, z=6, x+y=1;
б)  , где V: x2+y2+z2=1
, где V: x2+y2+z2=1
17.а)  , где V: x=0, y=0, z=0, z=5, x+y=1;
, где V: x=0, y=0, z=0, z=5, x+y=1;
б)  , где V: x2+y2=R2, x2+y2+z2=R2, z>0
, где V: x2+y2=R2, x2+y2+z2=R2, z>0
18.а)  , где V: x=0, y=0, z=0, x+y=3, x+y+z=5;
, где V: x=0, y=0, z=0, x+y=3, x+y+z=5;
б) 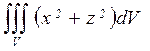 , где V: x2+z2=2y, y=2
, где V: x2+z2=2y, y=2
19.а)  , где V: x=0, y=0, z=0, x=2, z=2-y;
, где V: x=0, y=0, z=0, x=2, z=2-y;
б)  , где V: x2+y2=2x, z=0, z=a (a>0)
, где V: x2+y2=2x, z=0, z=a (a>0)
20.а)  , где V:
, где V:  ;
;
б)  , где V: x=0, z=0, x=1, z=a, x2+y2=1
, где V: x=0, z=0, x=1, z=a, x2+y2=1
21.а)  , где V: x=0, y=0, z=0, y=a, x+z=a;
, где V: x=0, y=0, z=0, y=a, x+z=a;
б) 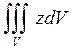 , где V:
, где V:  , z=1
, z=1
22.а) 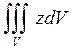 , где V: x=0.5, y=x, y=2x, z=0,
, где V: x=0.5, y=x, y=2x, z=0,  ;
;
б)  , где V: x2+y2=2x, z=0, z=1, y=0
, где V: x2+y2=2x, z=0, z=1, y=0
23.а) 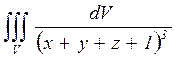 , где V: x=0, y=0, z=0, x+y+z=1;
, где V: x=0, y=0, z=0, x+y+z=1;
б)  , где V: x2+y2=2x, z=0, z=3, y=0
, где V: x2+y2=2x, z=0, z=3, y=0
24.а) 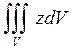 , где V: x=0, y=0, z=0, x+y+z=2;
, где V: x=0, y=0, z=0, x+y+z=2;
б)  , где V: x2+y2=z2, x2+y2+z2 =2Rz
, где V: x2+y2=z2, x2+y2+z2 =2Rz
25.а)  , где V:
, где V:  ;
;
б) 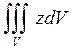 , где V: x2+y2-z2 =0, z=2
, где V: x2+y2-z2 =0, z=2
26.а)  , где V: x=0, y=1, z=0, y=3, x+2z=3;
, где V: x=0, y=1, z=0, y=3, x+2z=3;
б)  , где V: z=6-x2-y2, x2+y2=z2
, где V: z=6-x2-y2, x2+y2=z2
27.а)  , где V: x=0, y=0, z=0, y=a, x+z=b (a>0, b>0);
, где V: x=0, y=0, z=0, y=a, x+z=b (a>0, b>0);
б)  , где V: x2+y2+z2=4, y=0, 2x2=x2+y2,
, где V: x2+y2+z2=4, y=0, 2x2=x2+y2, 
28.а)  , где V: x=0, y=0, z=0, z=3, x+y=1;
, где V: x=0, y=0, z=0, z=3, x+y=1;
б)  , где V: x2+y2=hz, z=h.
, где V: x2+y2=hz, z=h.
29.а)  , где V: x2+y2-z2 =1,
, где V: x2+y2-z2 =1,  ;
;
б)  , где V: x2+y2=2z, z=2.
, где V: x2+y2=2z, z=2.
30.а) 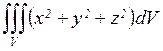 , где V:
, где V:  ;
;
б)  , где V: x2+z2=1, y=0, y=1.
, где V: x2+z2=1, y=0, y=1.
4*.С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями:
1. y=2-x, y2=4x+4 2. x=y2-2y, x+y=0
3.  (лемниската Бернулли) 4. y=4-x2, y=0
(лемниската Бернулли) 4. y=4-x2, y=0
5.  (четырехлепестковая роза) 6.
(четырехлепестковая роза) 6.  (трехлепестковая роза)
(трехлепестковая роза)
7.  (кардиоида) 8. y2=4+x, x+3y=0
(кардиоида) 8. y2=4+x, x+3y=0
9.  (четырехлепестковая роза) 10. xy=4, y=x, x=4
(четырехлепестковая роза) 10. xy=4, y=x, x=4
11. x2+y2=2x, x2+y2=4x, y=x,  12. y2=10x+25, y2=-6x+9
12. y2=10x+25, y2=-6x+9
13. y2=4ax, x+y=3a (a>0),  14. x=y, x=2y, x+y=a, x+3y=a, (a>0)
14. x=y, x=2y, x+y=a, x+3y=a, (a>0)
15.  (вне кардиоиды) 16.
(вне кардиоиды) 16.  (кардиоида)
(кардиоида)
17.  (трехлепестковая роза) 18.
(трехлепестковая роза) 18.  (один лепесток розы)
(один лепесток розы)
19.  (лемниската Бернулли) 20. y=lnx, x-y=1, y=-1
(лемниската Бернулли) 20. y=lnx, x-y=1, y=-1
21.  (вне круга) 22. xy=1, xy=8, y2=x, y2=8x
(вне круга) 22. xy=1, xy=8, y2=x, y2=8x
23. y=sinx, y=cosx,  24. 2xy=a2, xy=2a2, 2y=x, y=2x
24. 2xy=a2, xy=2a2, 2y=x, y=2x
25  (четырехлепестковая роза) 26.
(четырехлепестковая роза) 26. 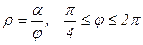
27.  (четырехлепестковая роза) 28.
(четырехлепестковая роза) 28. 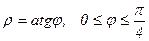
29.  . 30. y=x(x-1)2, y=0
. 30. y=x(x-1)2, y=0
5*.С помощью тройного интеграла вычислить объем тела, ограниченного следующими поверхностями:
1. x=0, y=0, z=0, x=4, y=4, z=x2+y2+1 2. x2+y2=9, z=y, z 
3. y=0, z=0, z=4, z=x2 4. x=9, x=z2+y2
5. z=x2+y2, z2 =x2+y2 6. z=12-x2-y2, z2 =x2+y2
7. x=0, y  , z=0, 3x+4y=12, z=9-y2 8. x=0, y=0, z=0, z=x2+y2, x+z=4
, z=0, 3x+4y=12, z=9-y2 8. x=0, y=0, z=0, z=x2+y2, x+z=4
9.  , z=x2+y2 10. z=1, x2+y2=16z
, z=x2+y2 10. z=1, x2+y2=16z
11. x+2y+z=4, y=0, z=0, x=2y2 12. x=0, y=1, z=0, y=3, x+2z=3
13. z  , 2x=x2+y2, z2 +x2+y2 =4 14. z=a, 2az=x2+y2
, 2x=x2+y2, z2 +x2+y2 =4 14. z=a, 2az=x2+y2
15. 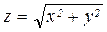 , z=3 16. z=0, z+x2+y2=1
, z=3 16. z=0, z+x2+y2=1
17. x=0, y=0, z=0, 2x+y=4, z=4-x2 18. z=0, z=a-x, y2=ax
19. x=0, y=0, z=0, x+y=4, z=x2+y2 20. x=1, 2x=z2+y2
21. x2+y2=ax, z2 +x2+y2 =a2, z  22. 3z=x2+y2, z2 +x2+y2 =4
22. 3z=x2+y2, z2 +x2+y2 =4
23. y=0, z=0, x+y+z=a, 3x+y=a, 1,5x+y=a 24. z=0, ax=x2+y2, 2az=x2+y2
25. z=0, y=1, z=x2+y2, y=x2 26. y=  , y=2
, y=2  , z=0, x+y=6 (y>0)
, z=0, x+y=6 (y>0)
27. az=y2, a2 =x2+y2, z  28. x2+y2=2ax, z2 =x2+y2, z
28. x2+y2=2ax, z2 =x2+y2, z 
29. 2(x2+y2)-z2=0, x2+y2-z2 =-a2 30. x2+y2 =a2, x2+y2-z2 =-a2
6**. Вычислить момент:
1. Найти полярный момент инерции однородной фигуры, ограниченной линиями x+y=3, x=0, y=0.
2. Найти момент инерции однородной фигуры, ограниченной линиями y=4-x2, y=0, относительно оси OX.
3. Найти момент инерции однородной фигуры, ограниченной линиями  , x+y=3, y=0, относительно оси OX.
, x+y=3, y=0, относительно оси OX.
4. Найти момент инерции однородного тела, ограниченного поверхностями x=0, y=0, z=0, x+y+z=1, относительно оси OX.
5. Найти момент инерции однородного тела, ограниченного поверхностями x=0, y=0, z=0, x+y+z=1, относительно оси OY.
6. Найти момент инерции однородного тела, ограниченного поверхностями x=0, y=0, z=0, x+y+z=1, относительно оси OZ.
7. Найти момент инерции однородного тела, ограниченного поверхностями x=0, y=0, z=0, x+y+z=1, относительно начала координат.
8. Найти статический момент однородного тела, образованного поверхностями x=0, y=0, z=0, x+y+z=5, относительно плоскости XOY.
9. Найти статический момент тела, образованного поверхностями x=0, y=0, z=0, x+y+z=5, относительно плоскости XOZ, если g(x,y,z)=x.
10. Найти статический момент тела, образованного поверхностями x=0, y=0, z=0, x+y+z=5, относительно плоскости YOZ, если g(x,y,z)=x.
11. Найти момент инерции однородной фигуры, ограниченной линиями 2y=x, x=a, y=a, x=0, относительно оси OX.
12. Найти момент инерции однородной фигуры, ограниченной линиями  , x+y=4, x=0, относительно оси OX.
, x+y=4, x=0, относительно оси OX.
13. Найти полярный момент инерции однородной фигуры, ограниченной линиями x+y=2, y=0, x=0.
14. Найти момент инерции однородного тела, ограниченного поверхностями x=0, y=0, z=0, y=a, x+z=a, относительно оси OZ.
15. Найти статический момент однородной фигуры, ограниченной линиями
y2 =4x+4, y2 =-2x+4, относительно оси OY.
16. Найти момент инерции круглого цилиндра (высота h, радиус основания а) относительно оси, служащей диаметром основания цилиндра.
17. Найти полярный момент инерции однородной площади, ограниченной линиями y=0, x=0,  .
.
18. Найти статический момент пластинки в форме прямоугольного треугольника с катетами OA=a, OB=b относительно катета OA, если плотность ее в любой точке равна расстоянию от этой точки до катета OA.
19. Найти статический момент однородного тела, ограниченного поверхностями x=0, z=0, y=1, y=3, x+2z=3, относительно плоскости YOZ.
20. Найти статический момент однородного тела, ограниченного поверхностями x=0, z=0, y=1, y=3, x+2z=3, относительно плоскости XOZ.
21. Найти статический момент однородного тела, ограниченного поверхностями x=0, z=0, y=1, y=3, x+2z=3, относительно плоскости XOY.
22. Найти момент инерции однородного круга радиусом R относительно точки, лежащей на окружности.
23. Найти момент инерции равнобедренного треугольника с основанием а и высотой h относительно вершины.
24. Найти момент инерции однородного прямоугольника со сторонами а и b относительно точки пересечения диагоналей.
25. Найти момент инерции однородного тела, ограниченного поверхностями z=4, z=x2+y2, относительно оси OZ.
26. Найти статический момент однородного прямоугольника со сторонами а и b относительно стороны а.
27. Найти момент инерции однородного квадрата со стороной а относительно вершины.
28. Найти статические моменты однородного прямоугольного параллелепипеда с ребрами a,b,c относительно его граней.
29. Найти статический момент однородного круга радиусом R относительно касательной.
30. Найти статический момент однородного полукруга радиусом R относительно диаметра.
7*. Тело плотностью µ задано ограничивающими его поверхностями. Найти массу тела.
1. 
2. 
3. 
4. 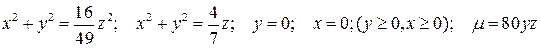
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 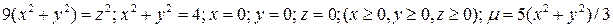
17. 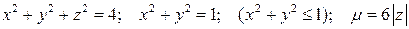
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 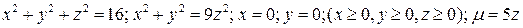
Дата добавления: 2015-10-13; просмотров: 235 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проверить, будет ли потенциальным и соленоидальным поле . | | | Как я с ней встретилась. |