Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Задание № 5. Найти наибольшее и наименьшее значение функции на заданном отрезке.

Читайте также:
  1. I тон сердца. Механизм образовани, диагностическое значение.
  2. I. Изменения, позволившие найти выход из тупика
  3. I. ПОНЯТИЕ И ФУНКЦИИ КОНФЛИКТА
  4. I. Функции и классификация органов чувств
  5. II. НАЗНАЧЕНИЕ, ОСНОВНЫЕ ЗАДАЧИ И ФУНКЦИИ ПОДРАЗДЕЛЕНИЯ
  6. III тон сердца. Понятие о ритме галопа. Диагностическое значение.
  7. IV. Термодатчики, их устройство и назначение.

Вариант№ 1.

Вариант№ 2.

Вариант№ 3.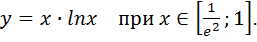

Вариант№ 4.

Вариант№ 5.

Вариант№ 6.

Вариант№ 7.

Вариант№ 8.

Вариант№ 9.

Вариант№ 10.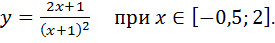

Вариант№ 11.

Вариант№ 12.

Вариант№ 13.

Вариант№ 14.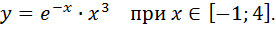

Вариант№ 15.

Вариант№ 16.

Вариант№ 17.

Вариант№ 18.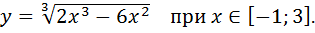

Вариант№ 19.

Вариант№ 20.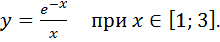

Вариант№ 21.

Вариант№ 22.

Вариант№ 23.

Вариант№ 24.

Вариант№ 25. .

Вариант№ 26. .

Вариант№ 27. .

Вариант№ 28. .

Вариант№ 29. .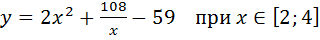

Вариант№ 30.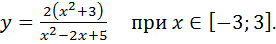

Тема 6. Функции многих переменных

Теоретические вопросы

1. Определение функции двух переменных. Область определения, график.

2. Поверхности второго порядка.

3. Частные производные.

4. Полный дифференциал функции двух переменных.

5. Неявные функции (определение, теорема существования).

6. Дифференцирование неявных функций.

7. Уравнение касательной плоскости и нормали к поверхности.

8. Дифференцирование сложной функции двух переменных.

9. Частные производные высшего порядка.

10. Локальный экстремум функции.

11. Условный экстремум функции.

12. Наибольшее и наименьшее значение функции в замкнутой области.

Варианты заданий

Дата добавления: 2015-10-13; просмотров: 106 | Нарушение авторских прав

Читайте в этой же книге: Задание №1. Решить задачи, используя скалярное произведение векторов. | Задание №2. Доказать, что векторы образуют базис и написать разложение вектора по векторам этого базиса. | Задание №4. Вычислить объем тетраэдра с вершинами в точках A, B, C, D и высоту, опущенную из вершины D на грань ABC. | Медианы, проведенной из вершины С. | Задание №5. Преобразовать уравнение кривой в полярной системе координат и построить кривую. | Задание №3. Решить систему уравнений с помощью обратной матрицы | Задание №3. Вычислить пределы, не пользуясь правилом Лопиталя | Задание №1. Найти производные функций | Задание №3. Найти частные производные от неявных функций | Задание №5. Исследовать заданную функцию на экстремум |
<== предыдущая страница | следующая страница ==>
Правила Лопиталя| Задание №1. Найти область определения функции. Ответ проиллюстрировать графически.
mybiblioteka.su - 2015-2024 год. (0.009 сек.)