Теорема Поклингтона и доказуемо простые числа общего вида на основании частичного разложения (n—1).

Теорема Сэлфриджа дает четкий критерий для проверки простоты числа n, однако требует знания полного разложения числа (n —1) на простые сомножители. Следующая теорема позволяет ограничиться частичной факторизацией (n —1).

Теорема Поклингтона.

Пусть n= RF+1, F= - каноническое разложение.

Если a: 1) a^{n —1}≡1(mod n);

2) 1(mod n) .

p ≡1(mod F) для любого простого p \ n.

■

Итак, если разложить n— 1 на два сомножителя n— 1=RF, где F> —1, то, если для некоторого a будут выполнены условия Теоремы Поклингтона (1) и (2), то n – простое.

Таким образом, можно значительно сократить количество проверок по сравнению с тестом Миллера.

Замечание.

Если n= RF+1 – нечетное простое число, F> —1, F= , НОД(R,F)=1, то вероятность того, что случайно выбранное 1 <a<n будет удовлетворять условиям (1), (2) теоремы Поклингтона, есть .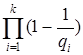

Дата добавления: 2015-09-07