Метод квадратичного решета.

Пусть n – число, которое надо факторизовать. Как и метод Ферма, данный метод ищет целые числа x, y: n=x ² —y ², но подход к поиску несколько иной. Поиск числа x осуществляется не среди всех чисел подходящего размера. Перед началом перебора производится отсев некоторых чисел.

Принцип отсева вытекает из следующих рассуждений: Возьмем небольшое число m и рассмотрим полную систему вычетов Z _m ={0, 1, 2, …, m —1}. Среди чисел из Z _m некоторые числа являются квадратами (то есть квадратичными вычетами), а другие не являются. Если m – простое число, то квадратов столько же, сколько неквадратов. Если m – составное, то квадратов несколько меньше. В общем случае,

P(s 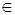Q(m)) ≤ .

Если число не является квадратичным вычетом по какому-то модулю m, то оно не является квадратом в Z, поэтому число y ² следует искать среди тех чисел, которые являются квадратами в Z _m.

В методе квадратичного решета берут несколько небольших попарно простых модулей m ₁, m ₂, …, m_k. Для каждого такого модуля составляют квадратичное решето (двоичный вектор S _m) следующим образом:

Для каждого x 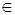Z _m вычисляют x ² mod m и z =(x ² —n) mod m. Если z является квадратом по модулю m, то S _m (x)=1, иначе S _m (x)=0. Проверка того, является ли z квадратом по модулю m, производится путем сверки с вычисленными x ² mod m.

X				…	m –1
x^2 mod m			2^2mod m	…	(m –1) ^2 mod m
z = x^2 – n mod m			z 2	…	zm —1

После того, как все решёта построены, начинается отсев кандидатов x. Решёта накладываются на последовательность чисел x от +1 до . Те числа, на которые наложился «0» хотя бы одного решета, отсеиваются. После отсева остается достаточно небольшое количество чисел – кандидатов в x. Для каждого такого числа вычисляется x ², z= x² – n и y= 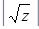. Если y ² =z, то числа a=x+y, b=x—y являются делителями числа n.

Пример:

n =279.

Построим решёта по модулям 4, 5 и 7:

x
x^2 mod 4
Z = x^2 –279 mod 4
S4

x
x^2 mod 5
z = x^2 –279 mod 5
S5

x
x^2 mod 7
z = x^2 –279 mod 7
S7

Теперь, когда мы построили три решета, наложим их на последовательность чисел от +1=17 до =140.

Поскольку 17 mod 4 = 1, то наложение решета S₄ начнем с S₄(1),

17 mod 5 = 2, то наложение решета S₅ начнем с S₅(2),

17 mod 7 = 3, то наложение решета S₇ начнем с S₇(3).

x

S4

S5

S7

Среди чисел от 17 до 34 остались 20, 22, 28,

Проверим их:

x =20, x ²=400, z=x ² —n =121, y = 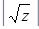=11, y ²=121= z.

Тогда a=x+y =31, b=x—y =9.

Ответ: 279=31·9.

Дата добавления: 2015-09-07