Символ Лежандра.

Символом Лежандра называется символ 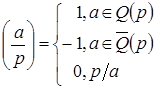(читается «символ Лежандра а по р»). а называется числителем, р – знаменателем символа Лежандра. Символ Лежандра отвечает на вопрос, является ли число а квадратичным вычетом по модулю р.

Вычислить символ Лежандра можно, пользуясь следующими свойствами.

Свойства символа Лежандра:

1. Критерий Эйлера: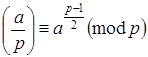

2. a≡a ₁(mod p)

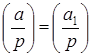
3.

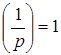
4.

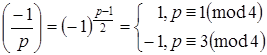
5.

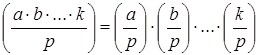
6.

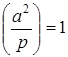
7.

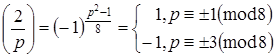
8. 3акон взаимности: если p, q – нечетные простые числа

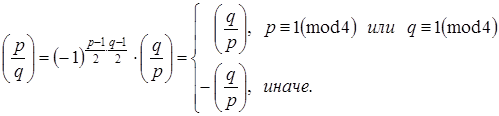
Свойства символа Якоби:

1. a ≡ a ₁(mod n)

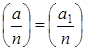
2.

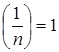
3.

4.

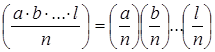
5.

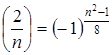
6. 3акон взаимности:

(n, m)=1, n, m >0, n, m — нечетные числа .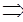

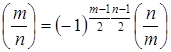Приведенные свойства символа Якоби позволяют составить алгоритм для вычисления символа Якоби и символа Лежандра:

1. Выделяем из числителя все степени двойки:

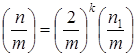
2. Пользуясь св-вом 4, понижаем степень k:

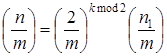
3. Если k mod 2=1, то вычисляем 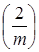пользуясь св-вом 5.

4. Символ 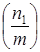преобразуем, пользуясь законом взаимности, и затем приводим числитель m по модулю знаменателя n ₁ и повторяя для получившегося символа Якоби шаги 1-4, пока в числителе не останется 1 или —1.

Символ Якоби отличается от символа Лежандра тем, что в первом знаменатель – составное число, а во втором – простое. Алгоритм вычисления символа Якоби и символа Лежандра одинаков, но для символа Якоби не выполняется критерий Эйлера.

Дата добавления: 2015-09-07