Квадраты и псевдоквадраты.

Пусть n – модуль RSA, то есть n=pq, p, q – различные большие простые числа.

Возьмем произвольное число a: (a, n)=1. Возможны следующие случаи:

1) . Тогда число a является квадратичным вычетом, или квадратом, по модулю n.

2) , , 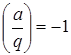или , 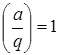. Тогда , и a не является квадратом по модулю n. То есть, не зная разложения модуля RSA на простые сомножители и получив отрицательное значение символа Якоби, можем с определенностью сказать, что a – не квадрат по модулю n.

3) , тогда a не является квадратом по модулю n, но символ Якоби, как и для квадрата по модулю n, равен единице: . То есть, не зная разложения модуля n на простые сомножители и получив положительное значение символа Якоби, не можем наверняка определить, является ли a квадратом по модулю n. Числа a: называются псевдоквадратами по модулю n=pq. Множество псевдоквадратов по модулю n обозначается .

Дата добавления: 2015-09-07