Вычисление кратных интегралов методом Монте-Карло. Начальное понятие числа

Содержание учебного материала

Вычисление кратных интегралов методом Монте-Карло.

2. Пример решения задачи в Mathcad.

3. Задание.

4. Список рекомендуемой литературы.

Вычисление кратных интегралов методом Монте-Карло. Начальное понятие числа

В случае когда, например, определенный интеграл не может быть вычислен в квадратурах, либо прибегают к численным методам интегрирования, либо расчет ведется с помощью метода Монте-Карло. Применение метода Монте-Карло становится оправданным при кратности интеграла больше трех. В данном примере мы используем метод Монте-Карло для расчета интегралов с кратностью не более трех. Это позволит более ясно представить технику применения метода.

Сначала рассмотрим вычисление простого определенного интеграла

(1)

где .

Введем под знак интеграла постоянный множитель (равный единице):

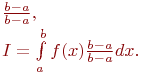
(2)

Вынесем из-под интеграла числитель дроби, получим

(3)

Как известно, если случайная величина распределена на заданном интервале (например, ) равномерно, то ее функция плотности обратно пропорциональна длине интервала, т. е.

Кроме того, если известно распределение случайной величины , то функция от этой случайной величины будет иметь тот же самый закон распределения. В этом случае математическое ожидание непрерывной равномерно распределенной случайной величины рассчитывается по формуле

Соответственно, математическое ожидание от функции случайной величины будет определяться следующим образом:

(4)

Сопоставляя (4) и (5), приходим к выводу, что определенный интеграл может быть рассчитан по формуле

(5)

Несмещенной оценкой математического ожидания случайной величины, как известно, является ее среднее арифметическое. Поэтому математическое ожидание можем приближенно найти по формуле

(6)

С учетом (6) получаем выражение для приближенного расчета определенного интеграла

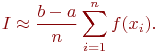
(7)

Чем больше число испытаний , тем точнее будет расчет математического ожидания (6) и, следовательно, определенного интеграла, вычисляемого по формуле (7).

Рассмотрим общий подход вычисления -кратного интеграла с помощью метода Монте-Карло.

Пусть задан -кратный интеграл вида

(8)

где подынтегральная функция задана на замкнутой области .

Погрузим область интегрирования в -мерный промежуток

(9)

имеющий меру

(10)

Определим в промежутке (10) функцию

(11)

Тогда в соответствии с (8) и (11) получим

(12)

Введем в рассмотрение -мерную случайную величину , имеющую в замкнутой области равномерное распределение вероятностей с дифференциальной функцией плотности

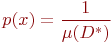
(13)

Функция плотности равномерного распределения есть величина постоянная, поэтому введем ее под знак интеграла (12) следующим образом:

(14)

Вынесем числитель дроби за знак интеграла, т. е.

((15)

В (15) -кратный интеграл — это математическое ожидание от функции случайной величины в предположении, что случайная величина распределена равномерно с плотностью (4.18). Следовательно, можем записать

(16)

где .

В свою очередь математическое ожидание может быть оценено с помощью арифметического среднего. Тогда приближенное значение -кратного интеграла будет определяться приближенной формулой

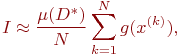
(17)

где — значение случайной величины в -м испытании.

Чтобы смоделировать выборку -мерной случайной величины , равномерно распределенной в -мерном промежутке , используются псевдослучайные числа. Для этого в каждом испытании с номером выбирают псевдослучайных чисел 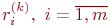, и по ним определяют координаты случайной величины , псевдослучайной точки .

Таким образом, техника применения метода Монте-Карло здесь будет заключаться в определении области , генерировании в ней псевдослучайных чисел, подсчета числа попаданий этих чисел в область и применении формулы (17).

Расчет площадей и объемов можно рассматривать как частный случай вычисления кратных интегралов. Например, вычисление объема тел с помощью трехкратного интеграла сводится к взятию интеграла по области при подынтегральной функции, тождественно равной единице.

Дата добавления: 2015-09-06