
|
Читайте также: |
Задача: Вычислить приближенное значение интеграла  , используя метод Монте-Карло, при n=1000000.
, используя метод Монте-Карло, при n=1000000.
Решение: Реализация метода Монте-Карло для вычисления интеграла представлена на рисунке:
a:=0 b:=1 n:= 1000000


I:=0…n
X i:=a+(b-a).md(1)
I:=  )
)
I = 0.285550681
Задание:
1. Внимательно изучите предложенный Вам материал и составьте конспект.
2. Ответьте на следующие вопросы:
2.1. В чём заключается основная идея метода Монте-Карло.
2.2. Какова графическая интерпретация метода Монте-Карло.
3. Вычислите приближённое значение интеграла заданной функции f (x) на отрезке [a,b] методом Монте-Карло.
Варианты заданий для выполнения практической части самостоятельной работы
| № | f(x) | [a,b] |
| 1. | 
| [0;3] |
| 2. | sin(2x2+1) | [0;1] |
| 3. | (x+1,9)  sin( sin(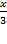 ) )
| [1;2] |
| 4. | 
| [2;3] |
| 5. | 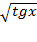
| [0;0,5] |
| 6. | 2,6 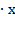 2 2 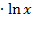
| [1,2;2,2] |
| 7. | (x2+1) 
| [0,5;1,5] |
| 8. | x2 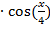
| [2;3] |
| 9. | 3x+ln(x) | [1;2] |
| 10. | 3x2 
| [-0,5;0,5] |
| 11. | 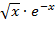
| [0,1;1,1] |
| 12. | 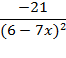
| [-2,0] |
| 13. | 
| [0;1] |
| 14. | 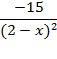
| [3;5] |
| 15. | 
| [2;3] |
Список рекомендуемой литературы:
Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad, стр. 308-313
Дата добавления: 2015-09-06; просмотров: 140 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление кратных интегралов методом Монте-Карло. Начальное понятие числа | | | ДЕЛОВАЯ ИГРА |