Решить задачу на построение. I. Анализ: Пусть АВС –искомый

Дано: А, С, АМ

Построить: 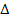АВС

I. Анализ: Пусть 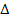АВС –искомый. По двум данным углам можно построить бесконечное множество подобных треугольников. Этот факт будет использоваться при построении вспомогательного треугольника. Сначала построим 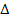АВ₁С₁ ( С₁= С), проведем в нем медиану АМ₁. У данного треугольника и искомого одинаковые формы. Затем на медиане АМ₁ отложим медиану АМ. И с помощью гомотетии с центром в точке А и 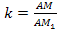построить точки В и С.

II. Построение:

1)

2) А₁, С₁ | А₁,С₁

3) С₁АН | С₁АН= А

4) АС₁К | АС₁К= С

5) В₁ | В₁=[AH) 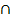[CK)

6) M₁ | B₁M₁=M₁C₁

7) [AM₁]

8) [AМ] | [AМ] 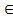[AM₁)

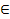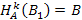9) В | B [AH), , где

10)C | C 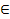[AC₁), , где

11) 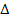АВС – искомый.

III. Док-во:

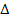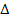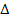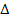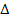По построению АВС подобен АВ₁С₁. Отсюда вытекает, что АМ – медиана АВС (т.к. АМ₁- медиана АВ₁С₁); С –равен данному углу(т.к. по построению С₁= С). Следовательно, АВС - искомый.

IV. Исследование:

Т.к. точки А и С₁ выбраны произвольно, то существует бесконечно много треугольников, удовлетворяющих двум данным углам. Но все эти треугольники будут подобны друг другу. Учитывая что пункт 8 выполняется однозначно, то такой треугольник будет единственным.

Метод решения задачи:

В данной задачи целесообразно в качестве метода решения выбрать метод подобия, с использование гомотетии с центром в точке А и коэффициентом k.

Возможны затруднения:

1) при выборе метода построения

2) При использовании гомотетии в построении (выбор коэффициента гомотетии)

3) при доказательстве единственности решений.

Дата добавления: 2015-09-07