Решить задачу.

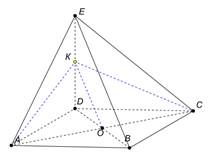Дано: ЕАВСД – пирамида (АВ=ВС=СД=АД=4, 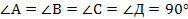), (ЕАД) 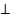(АВСД), (ЕДС) 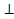(АВСД),

ВД=АС=ЕД.

Найти: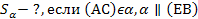

Решение:

I. построение:

1)

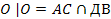
2)

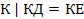
3) (ОК)

II. Доказать, что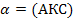

1) (АЕД) 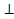(АВСД) (по усл), (ЕДС) 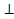(АВСД) (по усл)

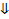
ЕД 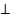(АВСД) (по теореме о двух пересекающихся плоскостях, перпендикулярных третьей плоскости)

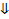
ЕД – высота ЕАВСД

2) О=АС 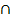ДВ (по построениею)

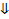
ДО=ОВ (т.к. АВСД – квадрат)

ДК=КЕ (по построению)

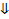
ОК- средняя линия ЕДВ (по определению средней линии треугольника)

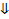
ОК 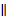ЕВ (по теореме о средней линии треугольника)

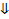
ВЕ (АСК) (по теореме о параллельности прямой и плоскости)

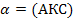
III. Вычисления:

1) АС -? АС –диагональ АВСД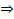

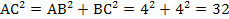
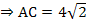
2) КО-? Рассм 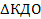: КД = ДО =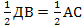

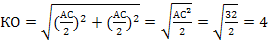
3)

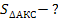
АК=КС (т.к. 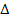АКД= 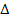КДС (по двум сторонам и углу между ними))

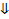
КО-высота 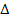АКС

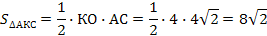
Ответ: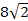

Теоретические основы решения:

1) теорема о двух пересекающихся плоскостях, перпендикулярных третьей плоскости

2) теорема о параллельности прямой и плоскости

3) определение средней линии треугольника

4) теорема о средней линии треугольника

5) определение квадрата

6) первый признак равенства треугольников

7) формула площади треугольника

8) теорема Пифагора

Затруднения возможны:

1) При построении сечения пирамиды

2) при построении пирамиды с двумя пересекающимися гранями, перпендикулярных основанию

3) при нахождении площади треугольник

Дата добавления: 2015-09-07