
Читайте также:
|
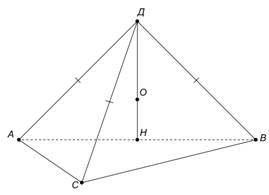 Дано: ДАВС – пирамида (ДА=ДВ=ДС), АВ=10, АС=6, ВС=8, ДН=1.
Дано: ДАВС – пирамида (ДА=ДВ=ДС), АВ=10, АС=6, ВС=8, ДН=1.
Найти:  -?
-?
Решение:
1) ДА=ДС=ДВ (по условию)
Н – центр описанной около  АВС окружности
АВС окружности
2) 
 АВС –прямоугольный (
АВС –прямоугольный ( С=90º)
С=90º)
Н – середина АВ
2) центр описанного шара лежит на перпендикуляре к плоскости основания, проведенном через центр окружности, описанной около основания пирамиды
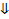
О – центр описанного шара, О 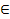 ДН,
ДН,
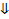

О 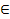 (ДАВ)
(ДАВ)

О – центр окружности, описанной около  ДАВ.
ДАВ.
Вычисления:
R -?
 ,
, 


Ответ: 13.
Теоретические основы решения:
1) определение центра описанной около треугольника окружности
2) определение центра описанного шара
3) формулы площади треугольника
4) теорема Пифагора
Затруднения возможны:
1) при построении треугольника основания (можно не учесть, что треугольник прямоугольный)
2) при решении того, что Н – центр описанной около основания окружности
3) при нахождении центра шара
Дата добавления: 2015-09-07; просмотров: 147 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решить задачу. | | | Решить задачу на построение. |