
Читайте также:
|
Дано: ЕАВСД – пирамида, Р 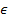 (ЕАВ), Т
(ЕАВ), Т 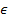 (ЕАД), М
(ЕАД), М 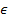 (ЕСД).
(ЕСД).
Построить: 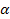 |
| 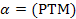

| Построение | Методический комментарий |
| 1) ЕАВСД | - строим пирамиду ЕАВСД |
2) 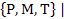 Р Р 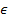 (ЕАВ), Т (ЕАВ), Т 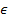 (ЕАД), М (ЕАД), М 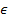 (ЕСД) (ЕСД)
| - отмечаем данные точки, лежащие в соответствующих гранях |
3)  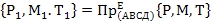
| - строим проекции точек Р, Т, М на плоскость (АВСД), приняв вершину Е за центр проектирования |
4) Х | Х=(РТ) 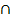 ( ( )
5) У | У=(МТ) )
5) У | У=(МТ) 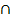 ( ( ) )
| - находим две точки основного следа плоскости (РТМ). |
| 6) (ХУ) – след | - прямая (ХУ) основной след секущей плоскости (РМТ) |
7) Z | Z=(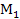 Д) Д) 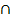 (ХУ) (ХУ)
| - построим след секущей плоскости на (ЕД). Для этого найдем точку Z, в которой прямая (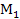 Д) пересекает след (ХУ) Д) пересекает след (ХУ)
|
8) (ZМ)
9) К | К=(ZМ) 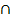 (ЕД) (ЕД)
| - проведем (ZМ) и получим точку К, в которой прямая (ZМ) пересекает (ЕД). Точка К является следом секущей плоскости на прямой (ЕД). |
10) N | N=(ZМ) 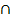 (ЕС) (ЕС)
| - проведем (ZМ) до пересечения с (ЕС) и получим точку N, являющуюся следом секущей плоскости на прямой (ЕС). |
11) (ТК)
12) R | R=(ТК) 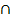 (ЕА) (ЕА)
| -т.к. точки Т и К лежат в одной плоскости, то можем провести прямую (ТК). При пересечении (ТК) с (ЕА) получим точку R, являющуюся следом секущей плоскости на прямой (ЕА). |
13) (RP)
14) F | F=(RP) 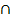 (ЕB) (ЕB)
| -т.к. точки R и P лежат в одной плоскости, то можем провести прямую (RP). При пересечении (RP) с (ЕB) получим точку R, являющуюся следом секущей плоскости на прямой (ЕB). |
| 15) (FN) | -т.к. точки F и N лежат в одной плоскости, то можем провести прямую (RP). |
16) 
| - многоугольник KNFR – искомое сечение |
Возможные затруднения:
1) При выборе метода построения сечения
2) При построении основного следа
3) При нахождении точек, являющимися следами секущей плоскости на соответствующих ребрах.
Дата добавления: 2015-09-07; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решить задачу. | | | Решить задачу. |