
Читайте также:
|
Дано: MN-сторона, PQ-меньшая диагональ,  =
=  (PN)^(PQ)
(PN)^(PQ)
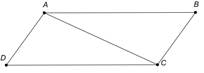
Построить: ABCD – параллелограмм. 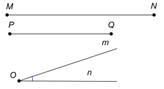
 I. Анализ.
I. Анализ.
Допустим, что АВСD – искомый, АВ=MN, AC=PQ,  ВАС=
ВАС=  mn. Мы видим, что в
mn. Мы видим, что в 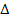 АВС даны три элемента. Это обстоятельство подсказывает следующий путь решения задачи: сначала нужно построить
АВС даны три элемента. Это обстоятельство подсказывает следующий путь решения задачи: сначала нужно построить 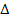 АВС по трем элементам, а затем достроить его до параллелограмма.
АВС по трем элементам, а затем достроить его до параллелограмма.
II. Построение:
 1)
1) 
2) [AB] | [AB]  , [AB]=[MN]
, [AB]=[MN]
3)  ВАM |
ВАM |  ВАM=
ВАM=  mn
mn
4) [AC] | [AC] 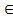 [AM), [AC]=[PQ]
[AM), [AC]=[PQ]
5) [CB]
6) 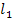 | C
| C 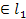 , (AB)||
, (AB)|| 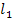 (//от точки С откладывается угол=
(//от точки С откладывается угол=  mn)
mn)
7) 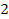 | A
| A  , (BC)||
, (BC)|| 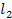 (//от точки А откладывается угол=
(//от точки А откладывается угол=  АСВ)
АСВ)
8) D | D= 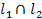
9) ABCD – искомый
III. Док-во:
По построению AB||CD, AD||BC, поэтому ABCD – параллелограмм.
Сторона АВ равна отрезку MN по построению, диагональ АС равна отрезку PQ по построению, а  ВАС=
ВАС=  mn, т.е. ABCD – искомый.
mn, т.е. ABCD – искомый.
IV. Исследование:
Ясно, что если по трем данным элементам можно построить треугольник, то можно построить и параллелограмм. При любых данных отрезках и данном неразвернутом угле такой треугольник построить можно. Следовательно, данная задача имеет единственное решение(т.к. прямую l и точку А можно выбрать произвольно, то существует бесконечно много треугольников, удовлетворяющих условию задачи. Все эти треугольники равны друг другу по первому признаку равенства треугольников, поэтому ед. решение).
Возможны затруднения:
1) При анализе того, что если построить треугольник, то можно построить и параллелограмм.
2) При построении параллельных прямых
3) при доказательстве единственности решений.
Дата добавления: 2015-09-07; просмотров: 115 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решить задачу. | | | Решить задачу на построение. |