
Читайте также:
|
10) Составить дисперcионный комплекс
| Показатели | Градации | Итого | |||
| х | у | z | |||
| Варианты | 0,348 0,864 1,707 4,884 7,778 9,130 9,785 | 0,965 0,914 0,829 0,512 0,222 0,087 0,022 | 4,826 4,586 4,146 2,558 1,111 0,435 0,108 | ||
Число вариант
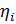
| N= 
| ||||
Сумма вариант в каждой градации
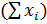
| 34,496 | 3,551 | 17,77 | 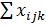 =55,817 =55,817
| |
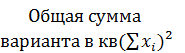
| 1189,97 | 12,6096 | 315,77 | 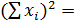 1518,35 1518,35
| |
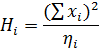
| 169,996 | 1,801 | 45,11 | 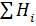 = 216,907 = 216,907
| |
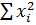
| 267,235 | 2,773343 | 69,489562 | 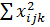 = 339,497 = 339,497
| |
11) 
12) Дисперсии
Общая:  339,497 – 148,4 = 191,097
339,497 – 148,4 = 191,097
Факториальная: 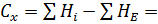 216,907 – 148,4 = 68,507
216,907 – 148,4 = 68,507
Остаточная:  339,497 – 216,907 = 122,59
339,497 – 216,907 = 122,59
13) Проверка правильности подсчетов
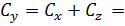 68,507 + 122,59 = 191,097
68,507 + 122,59 = 191,097
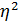 – показатель криволинейной связи между результативным признаком и воздействующим фактором
– показатель криволинейной связи между результативным признаком и воздействующим фактором
 ,
,  641
641
14) Достоверность факториальной дисперсии путем вычисления коэффициента Фишера
6.1 Число степеней свободы:
- для факториальной дисперсии: По формуле 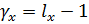
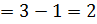
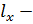 градации
градации
- для остаточной дисперсии: По формуле 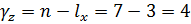
- для общей дисперсии: По формуле 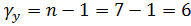
6.2 Девиата (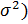 корректированная дисперсия
корректированная дисперсия
- факториальная девиата: По формуле 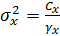
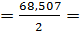 34,2535
34,2535
- остаточная девиата: По формуле  30,6475
30,6475
Коэффициент достоверности Фишера
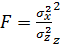 =1,118
=1,118
Сравнивают с таблицей Фишера
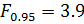
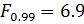
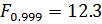 Если меньше - не достоверно
Если меньше - не достоверно
больше – достоверно
Ответ: Результаты Достоверны
№4 

| y | z | 
| 
| 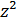
| xy | yz | xz |
| 0,721 1,790 3,537 10,116 16,111 21,596 24,167 | 2,428 2,321 2,146 1,488 0,889 0,340 0,083 | 12,139 11,665 10,732 7,442 7,444 1,702 0,417 | 0,519841 3,2041 12,510369 102,3334 259,5643 466,3872 584,0439 | 5,895184 5,387041 4,605316 2,214144 0,790321 0,1156 0,006889 | 147,355321 136,072225 115,175824 55,383364 55,413136 2,896804 0,006889 | 1,750588 3,2041 7,590402 15,052608 14,322679 7,34264 2,005861 | 29,473492 27,074465 23,030872 11,073696 6,617716 0,57868 0,034611 | 8,752219 20,88035 37,95908 75,28367 119,9303 36,7564 10,07764 |
| 78,038 | 9,695 | 51,541 | 1428,563 | 19,014495 | 512,303563 | 51,268878 | 97,883532 | 309,63966 |



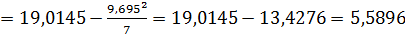





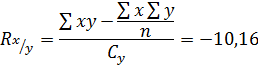





Ответ:
Дата добавления: 2015-09-07; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дисперсионный анализ | | | Дисперсионный анализ |