
Читайте также:
|
15) Составить дисперcионный комплекс
| Показатели | Градации | Итого | |||
| х | у | z | |||
| Варианты | 0,721 1,790 3,537 10,116 16,111 21,596 24,167 | 2,428 2,321 2,146 1,488 0,889 0,340 0,083 | 12,139 11,665 10,732 7,442 7,444 1,702 0,417 | ||
Число вариант
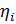
| N= 
| ||||
Сумма вариант в каждой градации
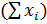
| 78,038 | 9,695 | 51,541 | 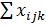 =139,274 =139,274
| |
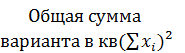
| 6089,93 | 93,993 | 2656,47 | 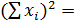 8840,393 8840,393
| |
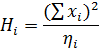
| 869,99 | 13,428 | 379,5 | 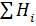 = 1262,918 = 1262,918
| |
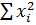
| 1428,563 | 19,014495 | 512,303563 | 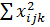 = 1959,881 = 1959,881
| |
16) 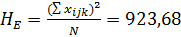
17) Дисперсии
Общая: 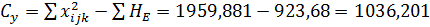
Факториальная: 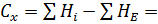 339,238
339,238
Остаточная:  696,963
696,963
18) Проверка правильности подсчетов
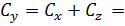 339,238+696,963= 1036,201
339,238+696,963= 1036,201
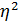 – показатель криволинейной связи между результативным признаком и воздействующим фактором
– показатель криволинейной связи между результативным признаком и воздействующим фактором
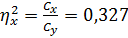 ,
, 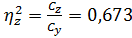
19) Достоверность факториальной дисперсии путем вычисления коэффициента Фишера
6.1 Число степеней свободы:
- для факториальной дисперсии: По формуле 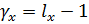
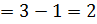
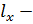 градации
градации
- для остаточной дисперсии: По формуле 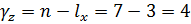
- для общей дисперсии: По формуле 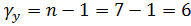
6.2 Девиата (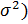 корректированная дисперсия
корректированная дисперсия
- факториальная девиата: По формуле 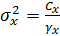
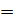 169,619
169,619
- остаточная девиата: По формуле 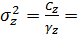 174,241
174,241
Коэффициент достоверности Фишера
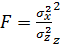 =0,973
=0,973
Сравнивают с таблицей Фишера
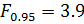
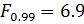
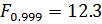 Если меньше - не достоверно
Если меньше - не достоверно
больше – достоверно
Ответ: Результаты Достоверны
Дата добавления: 2015-09-07; просмотров: 101 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дисперсионный анализ | | | На пути к Богу. |