
Читайте также:
|
6) Составить дисперcионный комплекс
| Показатели | Градации | Итого | |||
| х | у | z | |||
| Варианты | 0.224 0.556 1,098 2,143 4,091 4,551 | 0,478 0,444 0,390 0,286 0,091 0,045 | 2,389 2,222 1,951 1,429 0,455 0,285 | ||
Число вариант
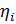
| N= 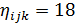
| ||||
Сумма вариант в каждой градации
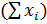
| 12,663 | 1,734 | 8,731 | 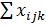 =23,128 =23,128
| |
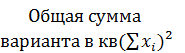
| 160,35 | 3,006756 | 76,23 | 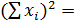 239,587 239,587
| |
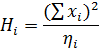
| 26,725 | 0,5011 | 12,705 | 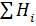 =39,9311 =39,9311
| |
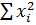
| 43,605 | 0,6698 | 16,7813 | 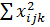 = 61,0561 = 61,0561
| |
7) 
8) Дисперсии
Общая: 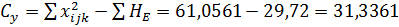
Факториальная: 
Остаточная: 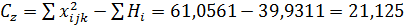
Проверка правильности подсчетов

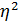 – показатель криволинейной связи между результативным признаком и воздействующим фактором
– показатель криволинейной связи между результативным признаком и воздействующим фактором
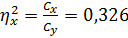 ,
, 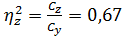
9) Достоверность факториальной дисперсии путем вычисления коэффициента Фишера
6.1 Число степеней свободы:
- для факториальной дисперсии: По формуле 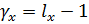
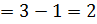
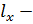 градации
градации
- для остаточной дисперсии: По формуле 
- для общей дисперсии: По формуле 
6.2 Девиата (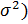 корректированная дисперсия
корректированная дисперсия
- факториальная девиата: По формуле 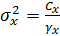

- остаточная девиата: По формуле 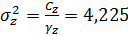
Коэффициент достоверности Фишера
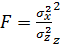 =1,21
=1,21
Сравнивают с таблицей Фишера
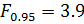
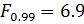
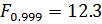 Если меньше - не достоверно
Если меньше - не достоверно
больше – достоверно
Ответ: Результаты Не Достоверны
№3 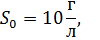

| y | z | 
| 
| 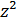
| xy | yz | xz |
| 0,348 0,864 1,707 4,884 7,778 9,130 9,785 | 0,965 0,914 0,829 0,512 0,222 0,087 0,022 | 4,826 4,586 4,146 2,558 1,111 0,435 0,108 | 0,121104 0,746496 2,913849 23,853456 60,497284 83,3569 95,746225 | 0,931225 0,835396 0,687241 0,262144 0,049284 0,007569 0,000484 | 23,290276 21,031396 17,189316 6,543364 1,234321 0,189225 0,011664 | 0,33582 0,789696 1,415103 2,500608 1,726716 0,79431 0,21527 | 4,65709 4,191604 3,437034 1,309696 0,246642 0,037845 0,002376 | 1,679448 3,962304 7,077222 12,493272 8,641358 3,97155 1,05678 |
| 34,496 | 3,551 | 17,77 | 267,235 | 2,773343 | 69,489562 | 7,777523 | 13,882287 | 38,881934 |

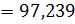

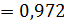


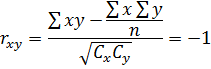
 1
1

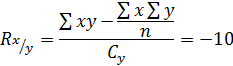
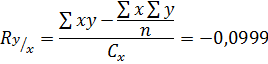
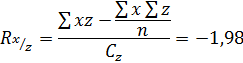
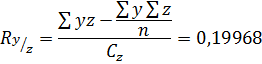
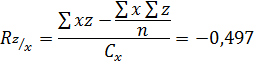

Ответ:
Дата добавления: 2015-09-07; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дисперсионный анализ | | | Дисперсионный анализ |