
Читайте также:
|
Определение показателей средних величин изменчивости и корреляций методом прямого анализа
№1 

| y | z | 
| 
| 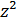
| xy | yz | xz |
| 0.124 0.309 0.490 0.690 0.787 0.962 | 0.088 0.069 0.051 0.031 0.021 0.004 | 0.438 0.346 0.255 0.155 0.107 0.019 | 0.015376 0.095481 0.2401 0.4761 0.619369 0.925444 | 0.007744 0.004761 0.002601 0.000961 0.000441 0.000016 | 0.191844 0.119716 0.065025 0.024025 0.011449 0.000361 | 0.010912 0.021321 0.02499 0.02139 0.016527 0.003848 | 0.038544 0.023874 0.013005 0.004805 0.002247 0.000076 | 0.054312 0.106914 0.12495 0.10695 0.084209 0.018278 |
| 3.362 | 0.264 | 1.32 | 2.37187 | 0.016524 | 0.41242 | 0.098988 | 0.082551 | 0.495613 |



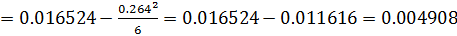



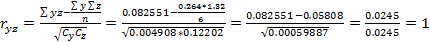


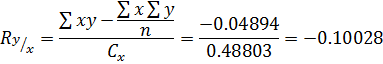




Ответ:
Определение показателей средних величин изменчивости
Для “x”
| № | х | х- 
| 
|
| 0,124 0,309 0,490 0,690 0,787 0,962 | -0,4363 -0,2513 -0,0703 0,1297 0,2267 0,4017 | 0,19035769 0,06315169 0,00494209 0,01682209 0,05139289 0,16136289 | |

| 3,362 | 0,0002 | 0.48802934 |



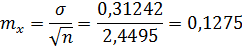

Ответ:  при
при 
(достоверно, так как 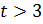 )
)
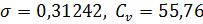 исходя из правил
исходя из правил  лимиты для генеральной совокупности составляет (0,56
лимиты для генеральной совокупности составляет (0,56  )
)
От -0,37726 до 1,49726
Для “y”
| № | y | y- 
| 
|
| 0.088 0.069 0.051 0.031 0.021 0.004 | 0.044 0.025 0.007 -0.013 -0.023 -0.04 | 0.001936 0.000625 0.000049 0.000169 0.000529 0.0016 | |

| 0.264 | 0.004908 |


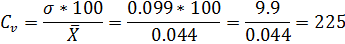

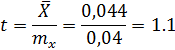
Ответ:  при
при 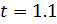
(не достоверно, так как 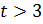 )
)
 исходя из правил
исходя из правил 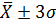 лимиты для генеральной совокупности составляет (0,044
лимиты для генеральной совокупности составляет (0,044  )
)
От -0,253 до 0,341
Для “z”
| № | z | z- 
| 
|
| 0.438 0.346 0.255 0.155 0.107 0.019 | 0.218 0.126 0.035 -0.065 -0.113 -0.201 | 0.047524 0.015876 0.001225 0.004225 0.012769 0.040401 | |

| 1.32 | 0.12202 |
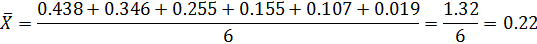
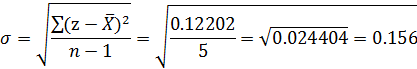


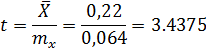
Ответ:  при
при 
(достоверно, так как 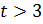 )
)
 исходя из правил
исходя из правил 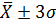 лимиты для генеральной совокупности составляет (0,22
лимиты для генеральной совокупности составляет (0,22  )
)
От -179312,87 до 179331,97
Дисперсионный анализ
1) Составить дисперcионный комплекс
| Показатели | Градации | Итого | |||
| х | у | z | |||
| Варианты | 0.124 0.309 0.490 0.690 0.787 0.962 | 0.088 0.069 0.051 0.031 0.021 0.004 | 0.438 0.346 0.255 0.155 0.107 0.019 | ||
Число вариант
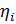
| N= 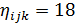
| ||||
Сумма вариант в каждой градации
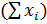
| 3.362 | 0.264 | 1.32 | 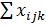 =4.946 =4.946
| |
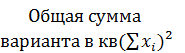
| 11.303 | 0.0697 | 1.7424 | 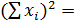 13.1151 13.1151
| |
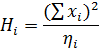
| 1.8838 | 0.0116 | 0.2904 | 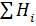 =2.1858 =2.1858
| |
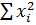
| 2.37187 | 0.016524 | 0.41242 | 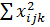 = 2.800814 = 2.800814
| |
2) 
3) Дисперсии
Общая: 
Факториальная: 
Остаточная: 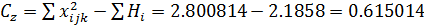
4) Проверка правильности подсчетов
 =1.441
=1.441
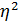 – показатель криволинейной связи между результативным признаком и воздействующим фактором
– показатель криволинейной связи между результативным признаком и воздействующим фактором
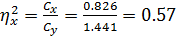 ,
, 
5) Достоверность факториальной дисперсии путем вычисления коэффициента Фишера
6.1 Число степеней свободы:
- для факториальной дисперсии: По формуле 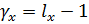
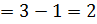
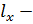 градации
градации
- для остаточной дисперсии: По формуле 
- для общей дисперсии: По формуле 
6.2 Девиата (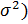 корректированная дисперсия
корректированная дисперсия
- факториальная девиата: По формуле 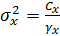
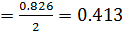
- остаточная девиата: По формуле 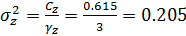
Коэффициент достоверности Фишера
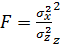 =
= 
Сравнивают с таблицей Фишера
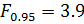
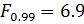
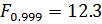 Если меньше - не достоверно
Если меньше - не достоверно
больше – достоверно
Ответ: Результаты Достоверны
№2 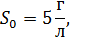

| y | z | 
| 
| 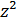
| xy | уz | xz |
| 0.224 0.556 1,098 2,143 4,091 4,551 | 0,478 0,444 0,390 0,286 0,091 0,045 | 2,389 2,222 1,951 1,429 0,455 0,285 | 0,050176 0,309136 1,205604 4,592449 16,736281 20,711601 | 0,228484 0,197136 0,1521 0,081796 0,008281 0,002025 | 5,707321 4,937284 3,806401 2,042041 0,207025 0,081225 | 0,107072 0,246864 0,42822 0,612898 0,372281 0,204795 | 1,141942 0,986568 0,76089 0,408694 0,041405 0,012825 | 0,535136 1,235432 2,142198 3,062347 1,861405 1,297035 |
| 12,663 | 1,734 | 8,731 | 43,605 | 0,6698 | 16,7813 | 1,97213 | 3,352324 | 10,133553 |











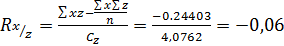
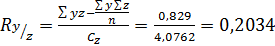


Ответ:
Дата добавления: 2015-09-07; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сергей Худиев | | | Дисперсионный анализ |