Матрица смежности

Матрица смежности – это матрица n × n, где n - число вершин. Строка с номером i содержит 1 в строке с номером j, если существует дуга из вершины i в вершину j.

Пример. Составить матрицу смежности для взвешенного графа:

Решение:

	a	b	c	d
a
b
с
d

Задание 1. Создать матрицу смежности для графа Невзвешенный граф можно интерпретировать как взвешенный, все ребра которого имеют одинаковый вес 1:

Решение:

	a	b	c	d
a
b
с
d

Небольшое затруднение возникнет в том случае, если в графе разрешаются ребра с весом 0. Тогда придется хранить два массива: один с нулями и единицами, которые служат показателем наличия ребер, а второй - с весами этих ребер.

Задание 2. Неориентированный граф задан матрицей смежности. Нарисовать граф.

Ответ:

Задание 3. Составить матрицу смежности для следующего графа:

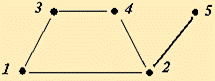
Ответ:

Матрица смежности для неориентированного графа будет симметричной относительно своей главной диагонали, а для орграфа - несимметричной.

Удобство матрицы смежности состоит в наглядности и прозрачности алгоритмов, основанных на ее использовании. А неудобство - в несколько завышенном требовании к памяти: если граф далек от полного, то в массиве, хранящем матрицу смежности, оказывается много "пустых мест" (нулей).

Дата добавления: 2015-10-13