Обход (поиск) в ширину

Обход графа в ширину (breadth first search, BFS) основывается на замене стека очередью:

1. Добавляет начальную вершину в очередь и помечает её как использованную.

2. Извлекает следующую вершину из очереди и добавляет в очередь смежные ей неиспользованные вершины, помечая их как использованные.

3. Если очередь не пуста, переходит к пункту 2.

После такой модификации чем раньше посещается вершина (помещается в очередь), тем раньше она используется (удаляется из очереди). Использование вершины происходит с помощью просмотра сразу всех еще не просмотренных вершин, смежных этой вершины. Таким образом, "поиск ведется как бы во всех возможных направлениях одновременно".[4]

Очередность просмотра вершин при поиске в ширину:

Пример:

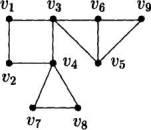
Порядок включения вершин при использовании метода поиска в ширину: v₁, v₂, v₃, v₄, v₇, v₈, v₆, v₅,v₉.

Писать поиск в ширину, как и большинство других алгоритмов, лучше для графа, заданного списком рёбер. В этом случае алгоритм более мобилен (это важно при модификациях) и даёт оптимальное время работы.

procedure bfs(v:integer);

var Og:array[1..nn]of integer;

yk1,yk2:integer;

i:integer;

Begin

// в элементе og[i] хранится номер группы вершины i. Изначально номер группы всех вершин кроме стартовой равен 0, это значит, что они ещё не были использованы.

for i:=1 to n do

og[i]:=0;

// Инициализация очереди, т.е. добавление в неё начальной вершины с номером v

yk2:=0;

yk1:=1;

Og[yk1]:=v;

used[v]:=true; // пометка вершины использованной

while yk2 < yk1 do // цикл работает, пока очередь не пуста

Begin

inc(yk2);v:=Og[yk2];

write(v:2);

// просматриваются все рёбра, исходящие из первой вершины очереди

for i:=1 to n do

// использована ли вершина, в которую ведёт выбранное ребро, если нет, то вершина добавляется в очередь

if (a[v,i] <> 0) and not used[i] then

Begin

// сдвигается указатель конца очереди

Дата добавления: 2015-10-13