Топологическая сортировка. Топологической сортировкой называют порядок нумерации вершин ориентированного

Топологической сортировкой называют порядок нумерации вершин ориентированного графа, при котором любое ребро идет из вершины с меньшим номером в вершину с большим.

Задача может быть сформулирована следующим образом: перечислить вершины графа в таком порядке, чтобы для любого ребра графа его начальная вершина была перечислена раньше конечной.

При помощи топологической сортировки строится корректная последовательность выполнения действий, всякое из которых может зависеть от другого: последовательность прохождения учебных курсов студентами, установки программ при помощи пакетного менеджера.

Топологическая сортировка существует для ациклических графов и не существует для циклических.

1. Помечаем все вершины графа как неиспользованные.

2. Ищем неиспользованную вершину, в которую не входит ни одно ребро (в соответствующем столбце матрицы смежности стоят только нули). Такая вершина всегда существует, если в графе нет контуров. Если такой вершины нет, то либо мы перебрали все вершины (топологическая сортировка закончена), либо в графе есть цикл (топологическая сортировка невозможна).

3. Помечаем найденную вершину как использованную, печатаем ее номер.

4. Удаляем из графа все ребра с началом в этой вершине (зануляется соответствующая строка матрицы смежности).

5. Переходим к шагу 2.

Для ускорения работы алгоритма можно хранить в массиве количество ребер, входящих в данную вершину, и обновлять это количество при удалении каждого ребра.

Задание 1.

Выполнить для графа, заданного с помощью матрицы инцидентности, топологическую сортировку.

Шаг 1. Проставляем степени вершин. Неиспользованная вершина, в которую не входит ни одно ребро – вершина №1. Записываем ее номер: 1. Удаляем из графа все ребра с началом в этой вершине.

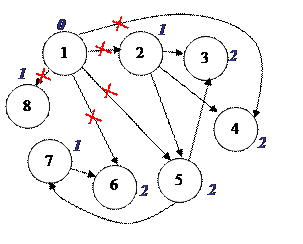
Шаг 2. Проставляем степени вершин. Неиспользованные вершины, в которые не входит ни одно ребро – вершины №2 и №8. Записываем номера: 2, 8 (предпочтение отдается вершине с меньшим номером). Удаляем из графа все ребра с началом в этой вершине.

Шаг 3. Проставляем степени вершин. Неиспользованные вершины, в которые не входит ни одно ребро – вершины №4 и №5. Записываем номера: 4, 5 (предпочтение отдается вершине с меньшим номером). Удаляем из графа все ребра с началом в этой вершине.

Шаг 4. Проставляем степени вершин. Неиспользованные вершины, в которые не входит ни одно ребро – вершины №3 и №7. Записываем номера: 3, 7 (предпочтение отдается вершине с меньшим номером). Удаляем из графа все ребра с началом в этой вершине.

Шаг 5. Проставляем степени вершин. Неиспользованная вершина, в которую не входит ни одно ребро – вершина №6. Записываем номер: 6. Удаляем из графа все ребра с началом в этой вершине.

Ответ: 1 | 2, 8| 4, 5| 3, 7| 6.

Дата добавления: 2015-10-13