Задача нахождения кратчайшего пути. Алгоритм Дейкстры

Пусть есть ориентированный граф, у которого все дуги имеют неотрицательные метки (стоимости дуг), а одна вершина определена как источник. Задача состоит в нахождении стоимости кратчайших путей от источника ко всем другим вершинам графа G (здесь длина пути определяется как сумма стоимостей дуг, составляющих путь). Эта задача часто называется задачей нахождения кратчайшего пути с одним источником.

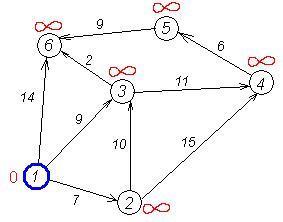
Пример [5]. Рассмотрим работу алгоритма Дейкстры на примере графа, показанного на рисунке. Пусть требуется найти расстояния от 1-й вершины до всех остальных. Кружками обозначены вершины, линиями — пути между ними (ребра графа).

В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1	Первый шаг. Минимальную метку имеет вершина 1. Ее соседями являются вершины 2, 3 и 6.
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до нее минимальна. Длина пути в нее через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7.	Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
	Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.
Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.	Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4. Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед вершины 2 — вершины 4 и 3. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22<∞, устанавливаем метку вершины 4 равной 22.	Ещё один сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.	Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты:
Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку 6, 4 и 5).

Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.

Поскольку алгоритм Дейкстры всякий раз выбирает для обработки вершины с наименьшей оценкой кратчайшего пути, можно сказать, что он относится к «жадным» алгоритмам.

Дан орграф G с множеством вершин V(G). Массив w — это двумерный массив стоимостей, где элемент w[i, j] равен стоимости дуги i ® j. Если дуги i ® j не существует, то w[i, j] ложится равным ¥, т.е. большим любой фактической стоимости дуг. В графе выделены две вершины, s и f, начало и конец пути.

В общем случае может существовать несколько различных путей из s в f. С каждой вершиной v графа связана переменная l[v], называемая меткой. На каждом шаге l[v] содержит длину текущего кратчайшего особого пути к вершине v. В процессе работы метка изменяется (временная метка). Метка становится постоянной, когда найден самый короткий путь от вершины s к вершине v. Алгоритм заканчивает работу, когда постоянной становится метка от s до f.

Переменная p принимает в качестве своих значений вершины графа. Н – множество вершин, имеющих временные метки.

Алгоритм Дейкстры:

procedure Short(s, f);

...

Begin

for v Î V(G) do l[v]:= ¥; { инициализация l }

l[s]:=0;

p:=s; // рабочая переменная

H:=V(G)-s; // множество вершин, имеющих временные метки

While p <> f do begin

for v Î Out(p) Ç H do l[v]:= (min[l[v],l[p]+w[p,v]);

m:=f; // m – минимальная метка

for v Î H do if l[m]>l[v] then m:=v;

H:=H-m; p:=m;

end;

end;

Задание. Для ориентированного графа нарисовать матрицу смежности. Используя алгоритм Дейкстры, найти минимальные путь между вершиной №1 и всеми остальными. Выполнение алгоритма описать пошагово. В результате должен быть представлен сам путь (пути), а не только минимальные значения.

В начале l (метки вершин): Н ={2, 3, 4, 5}	p =1	¥	¥	¥	¥
Шаг 1 l (метки вершин): Н ={3, 4, 5}		{1, 2} p =2	¥	{1, 4}	{1, 5}
Шаг 2 l (метки вершин): Н ={ 3, 5}			{1, 2, 3}	{1, 4} p =4	{1, 5}
Шаг 3 l (метки вершин): Н ={5}			{1, 4, 3} p =3		{1, 4, 5}
Шаг 4 l (метки вершин): Н ={ }					{1, 4, 3, 5} p =5

Несложно внести изменения в алгоритм так, чтобы можно было определить сам кратчайший путь (т.е. последовательность вершин) для любой вершины. Для этого надо ввести еще один массив Р1 вершин, где P1[v] содержит вершину, непосредственно предшествующую вершине v в кратчайшем пути. В программе надо записать условный оператор с условием l[p]+w[p,v]<l[v], при выполнении которого элементу P1[v] присваивается значение p. После выполнения алгоритма кратчайший путь к каждой вершине можно найти с помощью обратного прохождения по предшествующим вершинам массива Р1.

Type graph=array [1..nn,1..nn] of integer;

procedure short(n:integer; // количество вершин

W:graph; // матрица смежности

s,f:integer; // начальная и конечная вершины

var length: integer; // длина пути

var Weight:real; //

var Path: array[1..NN] of integer);

Var

v,k,j,m:byte;

l:array[1..nn] of real; // метки

p1:array[1..nn] of integer;

p:integer; // рабочая переменная для вершин

H:Set Of byte; // множество вершин, имеющих временные метки

Begin

H:=[];

// инициализация l

For v:=1 to n do begin

l[v]:=MaxInt; H:=H+[v];p1[v]:=0;

End;

l[s]:=0; p:=s;

H:=H-[s];

// выбор из Н такой вершины, что значение l минимально

while p<>f do begin

for v:= 1 to n do

Дата добавления: 2015-10-13