Просмотр графа

Просмотр графа заключается в посещении всех вершин и дуг графа и выводе в стандартный файл всей информации о графе. Для непустого графа информация группируется по вершинам (списки смежности).

Procedure BrowseGraph(graph:refnode);

Var a:refarc;

Nn,na: integer; {счетчики количества вершин и дуг}

Begin

Nn:=0; na:=0;

while graph<>nil do

begin

writeln(‘Вершина ’, graph^.id,’ с весом ’,graph^.infnode);

writeln(‘Список дуг:’);

a:=graph^.arclist;

if a=nil then writeln(‘пуст’);

while a<>nil dobegin

writeln(‘Дуга к вершине ’, (a^.adj)^.id,’, вес дуги ’,a^.infarc);

na:=na+1;

a:=a^.next;

end;

nn:=nn+1;

graph:=graph^.next;

end;

writeln(‘В графе ’, nn, ‘вершин и ‘, na,’ дуг’)

end;

Обход графов

Просмотр заключается в посещении всех вершин и дуг графа выводе всей информации о графе.

Обход (поиск) в глубину

Метод поиска в глубину (depth first search, DFS) — обобщение метода обхода дерева в прямом порядке.

Обход в глубину[2] (называемый иногда стандартным обходом), есть обход графа по следующим правилам:

1. Добавляет начальную вершину в стек и помечает её как использованную.

2. Рассматривает верхнюю вершину стека и добавляет в стек первую попавшуюся смежную ей неиспользованную вершину, помечая её как использованную. Если такой вершины нет, извлекает вершину стека.

3. Если стек не пуст, переходит к пункту 2.[3]

Таким образом, этот алгоритм обходит все вершины, достижимые из начальной, и каждую вершину обрабатывает не более одного раза.

Текст процедуры обхода в глубину (рекурсивный вариант):

var a:array[1..nmax,1..nmax]of integer;// матрица смежности

used:array[1..nmax]of boolean; // список меток

n:integer; // количество вершин графа

procedure dfs(v:integer);

Var

i:integer;

Begin

used[v]:=true; // помещенная в стек вершина помечается использованной

for i:=1 to n do // рассматриваются все ребра, исходящие из этой вершины

// проверка, использована ли вершина, в которую ведет выбранное ребро, если да, то поиск продолжается из этой вершины.

if (a[v,i]=1)and(not used[i]) then

Dfs(i);

End;

...

dfs(X); // здесь X - номер начальной вершины

При выполнении обхода графа по этим правилам стремимся проникнуть "вглубь" графа так далеко, как это возможно, затем отступаем на шаг назад и снова стремимся пройти вперед и так далее.

Пример:

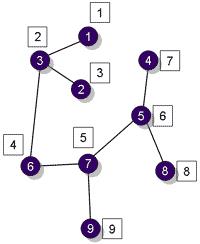
Для графа указать порядок включения вершин в множество достижимых вершин, если поиск начинается с вершины v1, при обходе в первую очередь предпочтение отдается вершине с меньшим номером.
	Ответ: v1, v2, v3, v4,v5, v6, v8,v9, v7.

Задание:

Неориентированный граф задан матрицей смежности. Нарисовать граф. Указать порядок включения вершин в множество достижимых вершин, если поиск в глубину начинается с вершины 1, при обходе в первую очередь предпочтение отдается вершине с меньшим номером.

Ответ:

Путь, полученный методом поиска в глубину, в общем случае не является кратчайшим путем из вершины v в вершину u.

Дата добавления: 2015-10-13