Теорема Крамера.

Формулы для вычисления длины вектора, скалярного и векторного произведений геометрических векторов в прямоугольной системе координат.

Даны два вектора с координатами a = (a_x;a_y;a_z), b = (b_x;b_y;b_z)

1. Длина вектора:

2. Вычисление скалярного произведения:

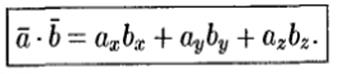
3. Вычисление векторного произведения:

Определение и свойства скалярного и векторного произведений

Определение обратной матрицы

Элементарные преобразования матриц

Алгебраическое дополнение к элементу квадратной матрицы

Ранг матрицы.

Рангом матрицы A (обозначается rang A) называется наибольший порядок порожденных ею определителей, отличных от нуля.

Теорема Крамера.

Если для системы линейных уравнений m = n и D¹0, то верны формулы Крамера для вычисления неизвестных x_i

где D - определитель основной матрицы системы

,

D_i - определители, которые получаются из D путем замены в нем i- ого столбца столбцом свободных членов исходной системы. Т.е.

Дата добавления: 2015-09-03