Определение определителя 2-го, 3-го порядка

Уравнение плоскости в пространстве.

1. Уравнение плоскости, проходящей через точку M₀(x₀;y₀;z₀) перпендикулярно вектору N= (A;B;C), который называется нормальным вектором плоскости.

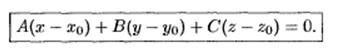
2. Общее уравнение плоскости.

3. Уравнение плоскости, проходящей через три точки M₁(x₁;y₁;z₁), M₂(x₂;y₂;z₂), M₃(x₃;y₃;z₃), не лежащие на одной прямой.

4. Уравнение плоскости в отрезках.

Уравнение прямой в пространстве.

1. Канонические уравнения прямой.

где M₀(x₀;y₀;z₀) – точка, принадлежащая прямой,

S= (m;n;p) – направляющий вектор прямой (т.е. вектор, параллельный этой прямой).

2. Параметрические уравнения прямой.

3. Уравнения прямой, проходящей через две точки M₁(x₁;y₁;z₁), M₂(x₂;y₂;z₂).

4. Общие уравнения прямой.

Прямая в пространстве задается как линия пересечения двух плоскостей.

Каноническое уравнение (и рисунок) эллипса, гиперболы и параболы.

1. Каноническое уравнение эллипса:

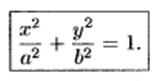
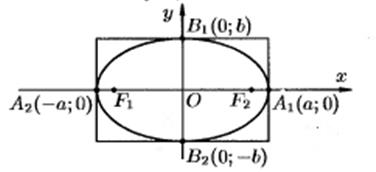
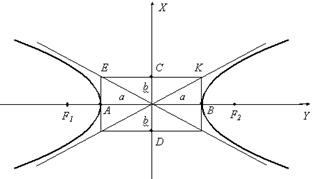
2. Каноническое уравнение гиперболы:

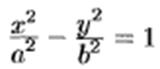
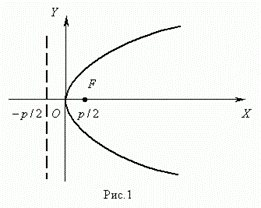
3. Каноническое уравнение параболы:

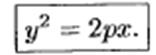
Дата добавления: 2015-09-03