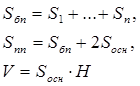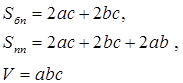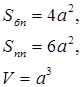Пряма призма

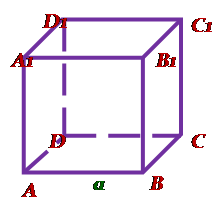
n-кутна	Прямокутний паралелепіпед	Куб
	A1 D1 A B C D B1 C1 a b c
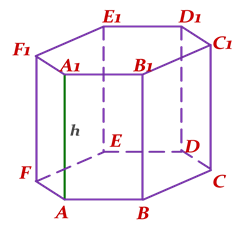
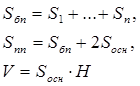
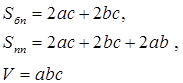
Основа – n-кутник, бічні грані – прямокутники, АА1 – висота,	Основа – прямокутник, бічні грані – прямокутники, АА1 – висота,	Основа – квадрат, бічні грані – квадрати, АА1 – висота,

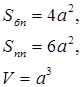
Наступний вид многогранників, які розглядаються, - піраміди. Уявлення про піраміду і деякі відомості про неї учні вже мають. Тому їх слід пригадати. Зокрема, піраміду вони розпізнають як многогранник, у якого одна грань – довільний многокутник, а решта граней – трикутники, що мають спільну вершину. Такий опис дає безпосереднє уявлення про форму всіх граней піраміди. Це значно полегшує сприймання форми піраміди, а отже, й дослідження її властивостей. При узагальненні поняття піраміди має бути сформульовано її означення.

З найпростішими тілами обертання учні ознайомленні у 5 – 6-х класах. У 9-му класі пропонується розглядати лише прямий круговий циліндр, прямий круговий конус, зрізаний конус і кулю.

Учні вже мають уявлення про те, як дістати поверхню циліндра обертанням прямокутника навколо однієї з його сторін та поверхню конуса обертанням прямокутного трикутника навколо одного з катетів.

Побудова зображень геометричних тіл – ефективний спосіб розвитку просторових уявлень. Побудова зображень циліндра, конуса, кулі не становить для учнів значних труднощів.

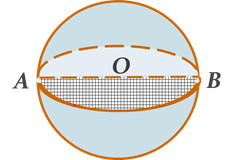
Після ознайомлення з паралельністю площин учні досить легко помічають, що основи циліндра знаходяться в паралельних площинах. Якщо каркасну модель циліндра розмістити в полі зору учнів так, що його основи матимуть вигляд еліпсів, а твірні та висота циліндра будуть вертикальними, то зрозумілим стає зображення циліндра.

Уявлення про осьовий переріз циліндра, конуса учні одержують у процесі ознайомлення з тілами обертання. Уже під час проведення досліду, який демонструє утворення циліндра, конуса, звертаємо увагу на те, що є їх осьовим перерізом. Під час побудови зображень цих тіл даємо уявлення також про зображення осьового перерізу.

З кулею учні ознайомленні раніше. У 9-му класі доцільно розглянути кулю як тіло, утворене обертанням півкруг навколо діаметра. Перед формулюванням означення кулі варто запропонувати учням пригадати означення кола і круга, відомі з курсу планіметрії. Тоді так само, як у випадку з циліндром і конусом, формулюється означення кулі.

Щоб дістати формули об’єму тіл обертання, можна провести три досліди з пересипання піску. У результаті пересипання піску із призми у циліндр дістанемо, що об’єм призми майже не відрізняється від об’єму циліндра, а при пересипанні піску із конуса в циліндр дістанемо, що об’єм конуса становить третину об’єму циліндра. Формулу об’єму кулі радіуса R дістанемо з формули об’єму відповідної півкулі. А її у свою чергу дістанемо, порівнюючи півкулю з конусом, який має радіус основи R і висоту R. У результаті пересипання піску з конуса в півкулю, дістанемо, що об’єм півкулі дорівнює об’єму чотирьох конусів.

Тіла обертання
циліндр	конус	куля
A11 A
АА1 – твірна і висота,	SA – твірна, SО – висота,

Учні 9-го класу готові до оволодіння вмінням виконувати такі зображення. Більшість з них правильно зображає прямокутний паралелепіпед, куб, піраміду, циліндр, конус, кулю, хоча поширеною помилкою є неправильне зображення невидимих ліній суцільною лінією.

Під час вивчення питань, пов’язаних із зображенням геометричних тіл, ефективним засобом є комп’ютер. За його допомогою легко виділити най значиміше, продемонструвати побудову зображення у відповідній послідовності у динаміці.

Дата добавления: 2015-08-21