Ошибка выборки.

Ошибка выборки —расхождение м.хар-ми выборочной и ге-неральн.совок-ти. ______

m=√d_о²/n

m--ошибка выборки,d_о²—дисперсия генеральн.совок-ти, n—объем выборки.

Не всегда возможно получить сведения о величине d_о² по изуч. явл-ю из предыдущ.с-ких исслед-й.Поэтому используют знач-е дисперсии выборки,к-рое меньше d_о².Д/этого использ-ся поправочный коэф-т к дисперсии выборки d_о²»d_о*(n/(n-1)).

Тогда: _____________

m=√(d_о² / n)(n / (n-1))

Коэф-т (n/(n-1)) часто опускается, т.к. при он при увеличении n быстро ®к единице.

Д/кол-го признака:

Д/кач-ного признака: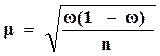

При бесповторной схеме отбора использ-ся поправочн.коэ-т (1-n/N).Тогда:

Ошибка выборки использ-ся д/ определения возможной величины данной хар-ки во всей совок-ти (z-m<ž<z+m).Рассматриваемая с-кая хар-ка имеет вероятностный хар-р.Указанным св-вом обеспеч-ся уровень вероят-ти p= 0,683.Д/повышения уровня надежности(доверия)надо увеличить пределы,в границах к-рых могут измен-ся знач-я изуч.хар-к.Ошибку выборки увеличивают в t раз. Предельная ошибка выборки: D=t´m(t—коэф-т доверия). Знач-е t д/соответ.уровня вероятности опред-ся по спец. таблицам.

ž®z ± t´m

Д/получения хар-ки изуч. совок-ти надо: 1. Получить знач-е этой хар-ки по данным выбо-рочн.набл-я. 2. Оценить среднюю ошибку выборки,т.е. возмож-ность отклонений этой величи-ны по всей совок-ти. 3. Исходя из целей с-кого исслед-я обосно-вать необходимый уровень веро-ятности. 4. Определить с учетом t предельную ошибку. 5. Исчис-лить изуч.хар-ку д/генеральн. совок-ти.

По своей сущности ст хар-ки имеют:

1.случайный характер.

2. м. Принимать разл. еначения в зав-сти от конкр. ед. генер. еовокуп., включеных в выборку

3. каждому из этих знач. соот-ний опред. вер-сть и определ. Ошибки выборки

4. ср. ошибка выборки явл-ся ср. квадрат. величины из отд. ошибок выборки взвешанных по вер-ям возникновения.

Дата добавления: 2015-08-21