
Читайте также:
|
5.1 Задача обработки результатов измерений: определить правильность выбора средства измерения по данным полученным в процессе контроля глубины 18+0,43 мм. Контроль осуществлялся глубиномером ГМ 25 ГОСТ 7470 с ценой деления 0,01мм.
5.2 Данные для обработки результатов измерений (результаты контроля) представлены в таблице 1.
Таблица 1 – Результаты контроля
В миллиметрах
Глубина, 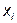
| ||||||
| 18,13 | 18,22 | 18,19 | 18,12 | 18,24 | 18,30 | 18,07 |
| 18,21 | 18,16 | 18,35 | 18,22 | 18,29 | 18,14 | 18,20 |
| 18,27 | 18,09 | 18,33 | 18,16 | 18,08 | 18,28 | 18,22 |
| 18,14 | 18,25 | 18,11 | 18,35 | 18,05 | 18,20 | 18,15 |
| 18,29 | 18,12 | 18,26 | 18,30 | 18,18 | 18,21 | 18,17 |
| 18,31 | 18,28 | 18,06 | 18,19 | 18,30 | 18,23 | 18,31 |
| 18,10 | 18,22 | 18,34 | 18,23 | 18,10 | 18,22 | 18,24 |
| 18,05 | - | - | - | - | - | - |
5.3 Порядок обработки результатов измерений:
а) найти точечные оценки закона распределения результатов измерений;
б) определить закон распределения случайных величин;
в) определить доверительные границы погрешности результатов измерений.
Методика обработки результатов измерений установлена в методических указаниях [5].
5.3.1 Нахождение точечные оценки закона распределения результатов измерений.
5.3.1.1 Определение среднего арифметического значения измеряемой величины, 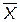 , мм, по формуле
, мм, по формуле
 , (1)
, (1)
где 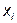 – значение измеряемой глубины, мм;
– значение измеряемой глубины, мм;
 – число значений в выборке.
– число значений в выборке.
В соответствии с данными таблицы 1 находим значения 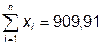 мм,
мм,  и определяем значение среднего арифметического по формуле (1)
и определяем значение среднего арифметического по формуле (1)
 мм.
мм.
5.3.1.2 Определение среднего квадратического отклонение (СКО), σ, мм, по формуле
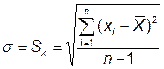 , (2)
, (2)
где  – оценка СКО, равная значению СКО, мм;
– оценка СКО, равная значению СКО, мм;
 - сумма квадратов разницы между значением измеряемой глубины и средним арифметическим значением, мм2.
- сумма квадратов разницы между значением измеряемой глубины и средним арифметическим значением, мм2.
Расчёт суммы квадратов разницы приведён в таблице 2.
Таблица 2
В миллиметрах
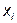
| 
| 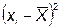
| 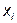
| 
| 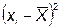
| 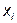
| 
| 
|
| 18,05 | 0,15 | 0,0225 | 18,12 | -0,08 | 0,0064 | 18,18 | 0,02 | 0,0004 |
| 18,05 | 0,15 | 0,0225 | 18,12 | 0,08 | 0,0064 | 18,18 | 0,02 | 0,0004 |
| 18,06 | 0,14 | 0,0196 | 18,13 | 0,07 | 0,0049 | 18,19 | 0,01 | 0,0001 |
| 18,07 | 0,13 | 0,0169 | 18,14 | 0,06 | 0,0036 | 18,19 | 0,01 | 0,0001 |
| 18,08 | 0,12 | 0,0144 | 18,14 | 0,06 | 0,0036 | 18,20 | ||
| 18,09 | 0,11 | 0,0121 | 18,15 | 0,05 | 0,0025 | 18,20 | ||
| 18,10 | 0,10 | 0,0100 | 18,16 | 0,04 | 0,0016 | 18,20 | ||
| 18,10 | 0,10 | 0,0100 | 18,16 | 0,04 | 0,0016 | 18,21 | 0,01 | 0,0001 |
| 18,11 | 0,09 | 0,0081 | 18,17 | 0,03 | 0,0009 | 18,21 | 0,01 | 0,0001 |
| 18,22 | 0,02 | 0,0004 | 18,25 | 0,05 | 0,0025 | 18,30 | 0,10 | 0,0100 |
| 18,22 | 0,02 | 0,0004 | 18,26 | 0,06 | 0,0036 | 18,31 | 0,11 | 0,0121 |
| 18,22 | 0,02 | 0,0004 | 18,27 | 0,07 | 0,0049 | 18,31 | 0,11 | 0,0121 |
| 18,22 | 0,02 | 0,0004 | 18,28 | 0,08 | 0,0064 | 18,33 | 0,13 | 0,0169 |
| 18,23 | 0,03 | 0,0009 | 18,28 | 0,08 | 0,0064 | 18,34 | 0,14 | 0,0196 |
| 18,23 | 0,03 | 0,0009 | 18,29 | 0,09 | 0,0081 | 18,35 | 0,15 | 0,0225 |
| 18,24 | 0,04 | 0,0016 | 18,29 | 0,09 | 0,0081 | 0,15 | 0,0225 | |
| 18,24 | 0,04 | 0,0016 | 18,30 | 0,10 | 0,0100 | - | - | - |
С учетом данных таблица 2 определяем СКО по формуле (2)
 мм.
мм.
5.3.1.3 Оценка среднего арифметического отклонения,  , мм, по формуле
, мм, по формуле
 , (3)
, (3)
По результату из 5.3.1.2 найдем значение среднего арифметического отклонения
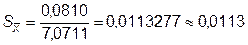 мм.
мм.
5.3.1.4 Проверка грубой погрешности с помощью критерия «Трёх сигм»
Критерий «Трех сигм»: практически все значения нормально распределённой случайной величины лежат в интервале  .
.
Формула для критерия «Трех сигм»:
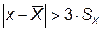 . (4)
. (4)
В соответствии с критерием «Трех сигм» в формулу (4) по очереди подставляем наименьшее ( ) и наибольшее (
) и наибольшее ( ) значение глубины из таблицы 1, соответственно получаем:
) значение глубины из таблицы 1, соответственно получаем:
а) при 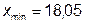 мм имеем
мм имеем  , что соответствует
, что соответствует  и позволяет сделать вывод, что наименьшее значение измеренной глубины не является промахом;
и позволяет сделать вывод, что наименьшее значение измеренной глубины не является промахом;
б) при 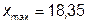 мм имеем
мм имеем  , что соответствует
, что соответствует  и позволяет сделать вывод, что наибольшее значение измеренной глубины не является промахом.
и позволяет сделать вывод, что наибольшее значение измеренной глубины не является промахом.
5.3.2 Определение закона распределения случайных величин.
5.3.2.1 Преобразуем результаты контроля из таблицы 1 в выборку, упорядоченную в порядке возрастания.
Упорядоченная выборка имеет вид: 18,05; 18,05;18,06;18,07;18,08; 18,09; 18,10; 18,10; 18,11; 18,12; 18,12; 18,13; 18,14; 18,14; 18,15; 18,16; 18,16; 18,17; 18,18; 18,18; 18,19; 18,19; 18,20; 18,20; 18,20; 18,21; 18,21; 18,22; 18,22; 18,22; 18,22; 18,23; 18,23; 18,24; 18,24; 18,25; 18,26; 18,27; 18,28; 18,28; 18,29; 18,29; 18,30; 18,30; 18,31; 18,31; 18,33; 18,34; 18,35;18,35 мм
5.3.2.2 Находим шаг гистограммы,  , мм, по формуле
, мм, по формуле
 , (5)
, (5)
где 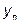 – последнее значение в выборке, мм;
– последнее значение в выборке, мм;
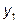 – первое значение в выборке, мм;
– первое значение в выборке, мм;
 – количество интервалов.
– количество интервалов.
Количество интервалов определяют исходя из условия, что  , должно находится в интервале между наибольшим значением и наименьшим значением, а также должно быть нечетным целым числом.
, должно находится в интервале между наибольшим значением и наименьшим значением, а также должно быть нечетным целым числом.
Наибольшее значение,  , определяем по формуле
, определяем по формуле
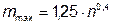 . (6)
. (6)
Наименьшее значение, 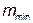 , определяем по формуле
, определяем по формуле
 . (7)
. (7)
С учетом формул (6) и (7) наибольшее и наименьшее значения соответственно равны:  ,
,  .
.
В соответствии с условием для количества интервалов принимаем число  .
.
Все значения для определения шага гистограммы найдены, следовательно, подставляем их в формулу (5) и определяем:
 мм.
мм.
5.3.2.3 Определение интервалов группирования 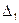 ,
,  ,
, 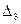 по формулам:
по формулам:
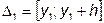 , (8)
, (8)
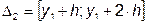 , (9)
, (9)
 . (10)
. (10)
Подставляя значения из 5.3.2.2 в формулы (8) - (10) получаем:
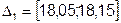 ,
,  ,
,  .
.
5.3.2.4 Определяем количество значений глубин ( ), входящих в каждый интервал группирования. Используя таблицу 1, получаем следующие значения
), входящих в каждый интервал группирования. Используя таблицу 1, получаем следующие значения  :
:
 ;
;  ;
;  .
.
5.3.2.5 Рассчитываем значение вероятности чего???
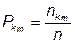 . (11)
. (11)
Используя найденные значения из 5.3.2.4, получаем следующие значения вероятности????:
 ;
;  ;
; 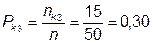 .
.
5.3.2.6 Строим гистограмму.
Для построения по оси х откладываем значения интервалов группирования 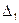 ,
,  ,
, 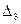 в порядке возрастания номеров и на каждом интервале строим прямоугольник высотой равной
в порядке возрастания номеров и на каждом интервале строим прямоугольник высотой равной  . Соединяем середины оснований каждого столбца гистограммы и получаем полигон, который представляет собой ломанную кривую (см. рисунок 1).
. Соединяем середины оснований каждого столбца гистограммы и получаем полигон, который представляет собой ломанную кривую (см. рисунок 1).

Рисунок 1 - Гистограмма и полигон
Вывод: форма гистограммы и полигона свидетельствует о нормальном законе распределения случайной погрешности в выборке.
5.3.3 Определение доверительных границ погрешности результатов измерений.
5.3.3.1 Определение доверительных границ случайной погрешности,  , мм, находим по формуле
, мм, находим по формуле
 при
при  , (12)
, (12)
где 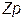 - квантильный множитель функции Лапласа, который определяется по справочным таблицам [8] и зависит от значения
- квантильный множитель функции Лапласа, который определяется по справочным таблицам [8] и зависит от значения  .
.
 , тогда
, тогда  и
и  .
.
5.3.3.2 Определяем систематическую погрешность, 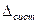 , мм.
, мм.
В качестве границы не исключённой систематической погрешности 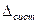 принимаем одно деление шкалы глубиномера ГМ 25 ГОСТ 7470, которое составляет 0,01мм.
принимаем одно деление шкалы глубиномера ГМ 25 ГОСТ 7470, которое составляет 0,01мм.
5.3.3.3 Находим значение расчётной погрешности,  , мм, по формуле
, мм, по формуле
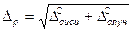 . (13)
. (13)
С учетом значений из 5.3.3.1 и 5.3.3.2 находим
 мм.
мм.
5.3.3.4 Результат измерения с учетом доверительных границ погрешности:
 мм, при
мм, при  .
.
5.3.3.5 Определяем нормируемую погрешность,  , мм, по справочным таблицам [12] для интервала размеров от 18 до 30 по 14 квалитету.
, мм, по справочным таблицам [12] для интервала размеров от 18 до 30 по 14 квалитету.
 мм.
мм.
5.3.3.6 Сравниваем значение расчетной и нормируемой погрешностей:  , т.е.
, т.е. 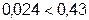 .
.
По результату из 5.3.3.6 делаем вывод по поставленной задаче обработки результатов измерений.
5.4 Вывод: в результате расчетов фактическая погрешность измерения составляет 0,024 мм, что не превышает нормируемую погрешность 0,43 мм, а значит средство измерения для контроля глубины (глубиномер ГМ 25 ГОСТ 7470 с ценой деления 0,01мм) выбрано правильно.
Дата добавления: 2015-08-21; просмотров: 62 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Приложение А | | | Перечень нормативных документов, используемых при оформлении чертежей |